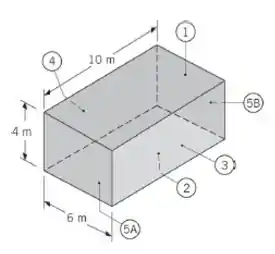
Uma sala é representada pela cavidade a seguir, onde o teto (1) tem uma emissividade de 0,8 e é mantido a 40°C por elementos aquecedores elétricos nele embutidos. Também são usados aquecedores para manter o piso (2), com emissividade de 0,9, a 50°C. A parede direita (3), com
emissividade 0,7, atinge uma temperatura de 15°C em um dia frio de inverno. A parede esquerda (4) e as paredes das extremidades (5A) e (5B) são isoladas termicamente. Para simplificar a análise, trate as duas paredes das extremidades como se elas fossem uma única superfície (5). Admitindo que as superfícies sejam cinzas e difusas, determine a transferência de calor por radiação líquida em cada superfície.
Passo 1
Shooow galerinha !! Vamos que vamos ...
O problema nos pediu para achar a transferência de calor por radiação líquida em cada superfície, certo?
Para a taxa de radiação liquida transferida em uma superfície podemos usar a seguinte relação:
Onde é a potência emissiva, a radiosidade, a área e a emissividade da superfície i.
Sabendo que a parede esquerda (4) e as paredes das extremidades (5) são isoladas termicamente:
Vamos dar uma olhada nas equações abertas?
O que nós sabemos é:
Então vamos começar pela parte fácil e achar as áreas?
As potências também são tranquilas para que possamos achar, basta lembrar que:
Lembrando que:
Então:
Passo 2
Quanto aos fatores de forma nós precisamos olhar as figuras abaixo:
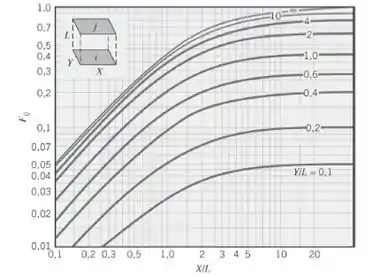
A primeira figura nós usamos para superfícies paralelas, ou seja, vamos achar Fazendo a razão como mostrado:
Olhando no gráfico e lembrando que a área da superfície 1 e 2 são iguais, a reciprocidade nos diz que:
No mesmo gráfico podemos achar Fazendo as novas razões:
Da mesma forma que antes:
Para as superfícies 1 e 3, e de maneira análoga para as superfícies 1 e 4, vamos olhar o segundo gráfico:
Dessa forma:
Como a superfície 1 ocorre de maneira similar à superfície 2:
Já achamos bastante, mas ainda falta, certo?
Vamos começar usando a relação da reciprocidade para achar e :
Substituindo:
Nós podemos usar outra relação para achar e :
Fizemos muito mais ainda não acabamos !! vamos usar novamente a reciprocidade para achar e
Substituindo:
Vamos fazer um resumão porque assim vai fica mais fácil:
Agora podemos substituir não é?
Passo 3
Agora podemos substituir não é ?!
Começando pela superfície 1:
Para a superfície 2:
Para a superfície 3:
Para a superfície 4:
Para a superfície 5:
Agora nós vamos utilizar um software para resolver estas cinco equações simultaneamente:
Passo 4
Shoow de bola galerinha !! Achamos as radiosidades e agora podemos achar o calor usando a primeira parte das equações acima!!
Começando pela superfície 1:
Para a superfície 2:
Para a superfície 3:
Para as superfícies 4 e 5 nós já sabemos:
E chegamos ao fim !!