Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 104

Um longo bastão uniforme com 50 mm de diâmetro e uma condutividade térmica de 15 W m K é aquecido internamente através de geração volumétrica de energia igual a 20 k W m 3 . O bastão está posicionado coaxialmente no interior de um tubo circular de maior diâmetro, 60 mm, cuja superfície é mantida a 500°C. Há vácuo na região anular entre o bastão e o tubo, e suas superfícies são difusas e cinzas, com emissividade de 0,2.

  1. Determine as temperaturas no centro e na superfície do bastão.
  2. Determine as temperaturas no centro e na superfície do bastão se o espaço anular estiver ocupado por ar atmosférico.
  3. Para diâmetros do tubo de 60, 100 e 1000 mm, e para as condições de vácuo e com ar atmosférico, calcule e represente graficamente as temperaturas no centro e na superfície do bastão como funções das emissividades superficiais, consideradas iguais, no intervalo entre 0,1 e 1,0.

Passo 1

É isso ai galerinhaaa !! Vamos continuando?

Bom, antes de qualquer coisa, o que queremos?

La letra (a) nós queremos achar a temperatura na superfície do bastão (1), T 1 , s , e no centro, T 1 , o .

Para o primeiro caso nós podemos utilizar a troca de calor por radiação entre o bastão e o tubo (2):

q ' 12 = σ T 1 , s 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 - ε 2 ε 2 A 2

Lembrando que a taxa de transferência de calor q ' 12 também pode ser escrito como:

q ' 12 = q ˙ π D 1 2 4

Igualando:

q ˙ π D 1 2 4 = σ T 1 , s 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 - ε 2 ε 2 A 2

Se:

A 1 = π D 1

A 2 = π D 2

Então:

q ˙ D 1 2 4 = σ T 1 , s 4 - T 2 4 1 - ε 1 ε 1 D 1 + 1 D 1 F 12 + 1 - ε 2 ε 2 D 2

Vamos ver o que sabemos?

ε 1 = ε 2 = 0,2

D 1 = 0,05   m

D 2 = 0,06   m

T 2 = 500 ° C + 273 =   773   K

σ = 5,67 × 10 - 8   W m 2 K 4

q ˙ = 20000 W m 3

Lembrando que:

F 12 = 1

Só nos resta substituir:

20000 0,05 2 4 = 5,67 × 10 - 8 T 1 , s 4 - 773 4 1 - 0,2 0,05 0,2 + 1 0,05 1 + 1 - 0,2 0,06 0,2

T 1 , s = 792   K

Passo 2

Para achar a temperatura no centro nós precisamos levar em conta apenas a condução!! E podemos usar a fórmula :

T 1 , o = q ˙ D 1 2 2 4 k + T 1 , s  

T 1 , o = q ˙ D 1 2 2 4 k + T 1 , s

Substituindo:

T 1 , o = 20000 0,05 2 4 15 + 792

T 1 , o = 792,21   K

Finalizamos a letra (a) !!

Passo 3

A letra (b) nos pede para determinar as temperaturas no centro e na superfície do bastão se o espaço anular estiver ocupado por ar atmosférico.

Para saber se há ou não condução precisamos saber se k e f f k < 1 , ok?

Sabendo que:

k e f f k = 0,386   P r 0,861 + P r 1 4 R a c 1 4

Vamos lembrar também que:

R a c = g β T 1 , s - T 2 L c 3 v α

L c = 2 ln ⁡ r e r i 4 3 r i - 3 5 + r e - 3 5 5 3

Sabendo que:

T 1 , s = 792   K

T 2 = 773   K

r i = 0,025   m

r 2 = 0,0 3   m

g = 9,81 m s 2

Olhando na Tabela A – 4 para achar as propriedades do ar a uma temperatura a 780 K:

v = 81,5 × 10 - 6 m 2 s

α = 11 5 , 6 × 10 - 6 m 2 s

k = 0,0563 W m K

β = 1 780 K

P r = 0,706

Substituindo:

L c = 2 ln ⁡ 0,03 0,025 4 3 0,025 - 3 5 + 0,03 - 3 5 5 3 = 0,0018   m

R a c = 9,81 1 780 792 - 773 0,0018   3 81,5 × 10 - 6 ( 115,6 × 10 - 6 ) = 0,142

k e f f k = 0,386   0,706 0,861 + 0,706 1 4 0,142 1 4 = 0,194

Então ocorre condução !!

Passo 4

Se a condução ocorre:

q ˙ π D 1 2 4 = q ' 12 + q ' c o n d

Nós já sabemos que:

q ' 12 = σ T 1 , s 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 - ε 2 ε 2 A 2 = 5,67 × 10 - 8 T 1 , s 4 - 773 4 1 - 0,2 0,05 0,2 + 1 0,05 1 + 1 - 0,2 0,06 0,2

q ' 12 = 5 4,4 × 10 - 8 T 1 , s 4 - 773 4

A condução neste caso é dada por:

q ' c o n d = 2 π k T 1 , s - T 2 ln ⁡ r e r i = 2 π 0,0563 T 1 , s - 773 ln ⁡ 0,03 0,025 = 1,94 T 1 , s - 773

Então:

20000 π ( 0,05 2 ) 4 = 54,4 × 10 - 8 T 1 , s 4 - 773 4 + 1,94 T 1 , s - 773

T 1 , s = 783   K

Usando a mesma relação do Passo 2:

T 1 , o = 20000 0,05 2 4 15 + 783

T 1 , o = 783 , 21   K

Passo 5

Terminamos a letra (b) e já seguimos para a (c)! Que é daquelas !!

Aqui nós vamos representar graficamente as temperaturas no centro e na superfície do bastão como funções das emissividades superficiais, variando entre 0,1 e 1,0, e calculando para três diâmetros diferentes, 60, 100 e 1000 mm.

Lançando estes dados no software:

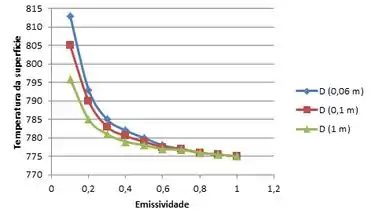
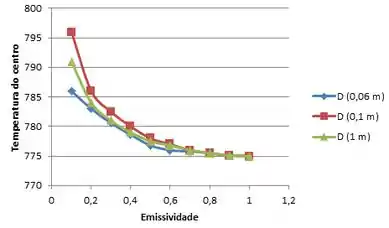
E é isso aí galerinha, chegamos ao fim de mais uma !!

Resposta

  1. T 1 , s = 792   K     |     T 1 , o = 792,21   K ;
  2. T 1 , s = 7 83   K     |     T 1 , o = 783 , 21   K ;
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um forno de secagem é constituído por um longo duto semicircular com diâmetro D=1m . Os materiais a serem secados cobrem a base do forno, enquanto a parede é mantida a 1200K . Qual é a taxa de secagem
Dois projetos de forno, como ilustrados e dimensionados no Problema 13.4, são usados para aquecer um corpo de prova em forma de disco ( A 1 ) . A potência fornecida aos fornos cônico e cilíndrico ( A
Um aquecedor tubular com a superfície interna negra de temperatura uniforme T s =1000K irradia um disco que se encontra em posição coaxial ao tubo.(a) Determine a potência radiante oriunda do aquecedo
Uma peça longa em forma de V é tratada termicamente pela sua suspensão no interior de um forno tubular com um diâmetro de 2m e uma temperatura de parede de 1000K . O V tem os lados com 1m de comprimen
Uma placa circular com 500m m de diâmetro é mantida a T 1=600K e está posicionada coaxialmente a uma peça com formato cônico. O lado superior do cone é isolado termicamente. A placa e o cone, cujas su