Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 113
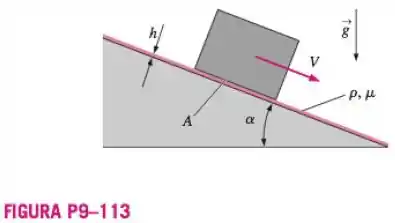
Um bloco desliza para baixo em uma parede longa, reta, inclinada, com a velocidade , sobre um filme fino de óleo de espessura (Figura P9-113). O peso do bloco é , e sua área de contato com a filme de óleo é . Suponha que seja velocidade medida, e , , o ângulo e a viscosidade também sejam conhecidos. A espessura do filme de óleo não é conhecida. Encontre uma expressão analítica exata para como uma função dos parâmetros conhecidos , , , e . Use análise dimensional para gerar uma expressão adimensional para como uma função dos parâmetros dados. Construa uma relação entre seus que corresponda à expressão analítica exata da parte .
Passo 1
Fala galera !!!
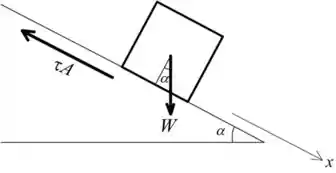
(a) Para resolver essa questão, precisamos supor que o fluxo seja incompressível, constante, newtoniano, laminar, paralelo e totalmente desenvolvido. Posemos desenhar o seguinte o diagrama do corpo livre do bloco.
Passo 2
Agora, vamos tomar a condição de equilíbrio das forças resultantes para dizer que
Ou seja:
Nos temos que é dados por . Log, temos que:
Portanto, a expressão para a espessura do óleo é
Passo 3
(b) Agora, queremos gerar uma expressão adimensional para como uma função dos parâmetros fornecidos. Existem seis parâmetros nesse problema, ou seja, .
Os seis parâmetros são:
Espessura do filme de óleo:
Velocidade:
Área:
Peso:
Ângulo:
Viscosidade dinâmica:
Passo 4
Aqui, o parâmetro é uma função de outros cinco parâmetros.
Agora, vamos escrever a dimensão primária de cada parâmetro.
Dimensão primária da espessura do filme:
Dimensão primária da velocidade:
Dimensão primária da área:
Dimensão primária do peso:
Dimensão primária do ângulo:
Dimensão primária da viscosidade:
O número de dimensões primárias representadas no problema é , então, como primeiro palpite, é o primeiro conjunto igual a três .
Passo 5
Se esse valor de estiver correto, o número previsto pelo teorema de Buckingham é
Desde que , temos que escolher três parâmetros repetidos. Com base nas diretrizes para a seleção de parâmetros repetidos, vamos escolher , e .
Passo 6
Agora, vamos combinar esses parâmetros repetidos com os outros parâmetros restantes a serem criados . Antes de tudo, um independente é gerado usando a variável independente .
Independente :
Temos que a dimensão primária de é:
Substituindo as dimensões de casa parâmetro na equação 1, temos:
Agora, vamos igualar os expoentes de cada dimensão primária independentemente para encontrar os valores de , e . Assim, temos:
Massa
Tempo
Comprimento
Com , e encontrados, vamos substituir na equação 1. Assim temos:
Portanto, temos que:
Passo 7
Agora, vamos gerar independente usando a variável independente .
Temos que a dimensão primária de é:
Substituindo as dimensões de casa parâmetro na equação 2, temos:
Agora, vamos igualar os expoentes de cada dimensão primária independentemente para encontrar os valores de , e . Assim, temos:
Massa
Tempo
Comprimento
Com , e encontrados, vamos substituir na equação 2. Assim temos:
Portanto, temos que:
Passo 8
Agora, vamos gerar independente usando a variável independente .
Temos que a dimensão primária de é:
Substituindo as dimensões de casa parâmetro na equação 2, temos:
Agora, vamos igualar os expoentes de cada dimensão primária independentemente para encontrar os valores de , e . Assim, temos:
Massa
Tempo
Comprimento
Com , e encontrados, vamos substituir na equação 3. Assim temos:
Portanto, temos que:
Passo 9
Das equações de , e a relação sem dimensão é:
Para colocar o da equação acima na forma da equação encontrada na letra , podemos fazer o seguinte:
Substituindo pelos resultados encontrados, temos:
Assim, vemos que a análise dimensional é realmente consistente com a solução exata. Obviamente, não poderíamos conhecer o relacionamento da equação acima apenas pelo raciocínio dimensional.
Portanto, a relação entre o é:
Resposta
(a)
(b)