Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 26
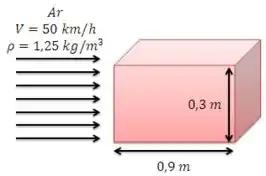
Os motoristas de táxis geralmente carregam sobre o teto de seus carros painéis de propaganda para obter uma renda extra, mas isso aumenta também o consumo de combustível. Considere um painel que consiste de um bloco retangular de de altura, de largura e de comprimento montado sobre o teto do carro de maneira que o painel tenha uma área frontal de por nos quatro lados. Determine o aumento no custo anual de combustível deste táxi devido a este display. Suponha que o táxi rode por ano a uma velocidade média de e que a eficiência global do motor seja . Considere a densidade, o preço unitário e o valor calórico da gasolina como , e , respectivamente, e a densidade do ar .
Passo 1
Temos um táxi com um display retangular de área projetada . Devido à força de arraste do ar sobre o display, o táxi dissipa uma energia por atrito. Devemos calcular o quanto isso gera de custo adicional em combustível por ano. Vamos lá?
Para começar, vamos determinar a magnitude da força de arraste. O coeficiente de arraste para uma geometria retangular e uma relação de largura e de comprimento:
A partir disso, podemos determinar a força de arraste pela relação:
Passo 2
Nosso próximo passo será calcular o trabalho realizado pelo táxi para vencer a força de arraste. Tudo bem?
Para isso, vamos usar uma velha conhecida:
Lembra dessa equação? Legal!
O táxi anda uma distância média de , então:
Este é o trabalho ideal que o carro realiza. Porém, como a eficiência do motor é de apenas , o trabalho real será:
Passo 3
Tudo bem até aqui?
Vamos agora calcular a quantidade de gasolina necessária para fornecer essa energia. A energia fornecida pela gasolina é:
Para converter em volume:
Por fim, vamos calcular o custo anual referente à esse consumo adicional de gasolina. Com o custo unitário de teremos um custo anual de:
Resposta
Aumento no custo anual: .