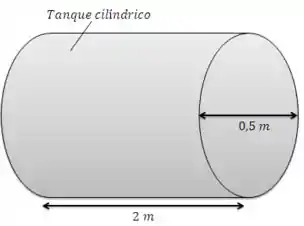
Pretende-se suprir as necessidades de água de um trailer instalando-se um tanque cilíndrico de de comprimento e de diâmetro sobre o teto do veículo. Determine a potência adicional necessária do trailer a uma velocidade de quando o tanque estiver instalado de forma que suas superfícies circulares estejam voltadas para (a) a frente e atrás do veículo e (b) os lados do veículo. Suponha que as condições atmosféricas sejam e .
Passo 1
Temos a instalação de um tanque cilíndrico no teto de um trailer. Devido à força de arraste do ar sobre o cilindro, o trailer precisará empregar uma potência adicional para se locomover. Tudo bem até aqui?
Vamos verificar como a disposição do cilindro influencia na força de arraste. Para começar, vamos reunir as propriedades do ar nestas condições. Pela Tabela :
O número de Reynolds para este escoamento é:
Tudo bem até aqui? Vamos agora verificar o que ocorre em cada situação.
Passo 2
No item (a), as superfícies circulares estão voltadas para a frente do veículo. Então, a área projetada é:
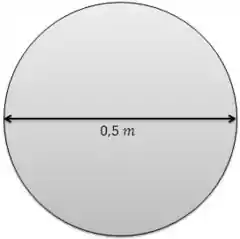
Como , o coeficiente de arraste para um cilindro horizontal é:
Para este caso, a força de arraste é:
Para finalizar, podemos obter a potência pela relação:
Passo 3
Vamos agora para o item (b). Neste caso, a área projetada é:
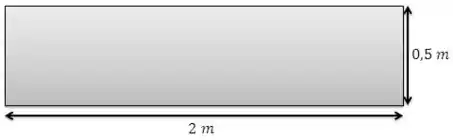
Como , o coeficiente de arraste para um cilindro vertical é:
Novamente, podemos calcular a força de arraste por:
Para finalizar, podemos obter a potência pela relação:
Resposta
(a) .
(b) .