Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 26

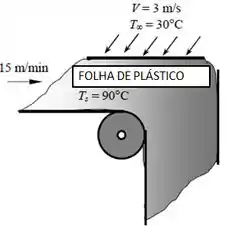
A seção de produção de uma fábrica de plástico produz uma folha contínua de plástico de 1,2m de largura e 2 mm de espessura, a uma taxa de 15m/min. A temperatura da folha de plástico é de 90°C quando exposta ao ar circundante. A folha é submetida ao escoamento de ar a 30°C com velocidade de 3 m/s em ambos os lados ao longo da superfície, na direção normal à direção do movimento da folha. A largura da seção de ar fria é tal que um ponto fixo sobre a folha de plástico passa através da seção em 2 s. Determine a taxa de transferência de calor a partir da folha de plástico para o ar.

Passo 1

Primeira coisa de sempre: vamos pegar os valores das propriedades do ar na temperatura Tf

T f = 90 + 30 2 60 ° C

ρ = 1,06 k g m 3

K = 0,0281 W m 2 ° C

v = 1,90   x   10 - 5   m 2 s

P r = 0,72

Agora, partiu calcular valor de Reynold...

R e L = V L v = 3   x   1,2 1,90   x   10 - 5 = 1,87   x   10 5

Ou seja, estamos abaixo do valor de Reynold crítico e portanto em regime laminar!

Passo 2

Vamos agora calcular o valor de h utilizando uma correlação apropriada ao problema, ok? As condições são: regime laminar, Ts constante e geometria de placa plana!

N u = h L K = 0,664 R e L 0,5 P r 1 / 3

h = K L 0,664 R e L 0,5 P r 1 / 3

h = 0,0281 1,2 0,664 1,87   x   10 5 0,5   x   0,72 1 3 = 6,0 W m 2 ° C

Ok, agora vamos usar a fórmula que representa a quantidade de calor que é trocada na forma de convecção.

NÃO ESQUECE QUE O PROBLEMA DEIXA BEM CLARO QUE O AR PASSA NAS DUAS SUPERFÍCIES DA PLACA, então você vai precisar multiplicar a área por 2!

OBS: Se fossem áreas diferentes você teria que somar qtotal = qconvA1 + qconvA2 onde A1 e A2 representam áreas distintas, beleza?

q = h 2 A T s - T ∞ = 2 L w h T s - T ∞

Putz!!! Precisamos do valor de w, né? Vem comigo pro passo 3!!

Passo 3

O enunciado nos deu a velocidade com que a folha é produzida e o tempo em que a folha permanece dentro da câmara de resfriamento, certo? Então com isso a gente consegue calcular o valor w, se liga!

∆ V = ∆ S ∆ t → ∆ S = ∆ V   x   ∆ t

Vamos passar a velocidade de produção para SI:

∆ V = 15 m m i n x 1   m i n 60 s = 0,25   m / s

Agora é só substituir e encontrar o valor de ΔS que no nosso caso equivale ao valor de w da folha, certo?

∆ S = 0,25   x   2 = 0,5   m

Passo 4

q = h 2 A T s - T ∞ = 2 L w h T s - T ∞ = 2 x   1,2   x   0,5   x   6   x   90 - 30 = 432   W

Resposta

q = 432   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A superfície superior de um compartimento aquecido possui uma porção muito lisa (A) e outra acentuadamente rugosa (B), e encontra-se em contato com uma corrente de ar atmosférico. Com o interesse de m
O teto do baú de um caminhão refrigerado é construído com um material composto, sendo constituído por uma camada de isolante de espuma de uretano (t2 = 50 mm, ki = 0,026 W/(m · K)) posicionada entre p
A camada-limite associada ao escoamento paralelo sobre uma placa isotérmica pode ser perturbada em qualquer posição x pelo uso de um fino fio que é esticado cruzando a largura da placa. Determine o va
Considere uma célula a combustível delgada com 50 mm × 50 mm similar a do Exemplo 1.5, com ar em escoamento paralelo sobre suas superfícies. Fios com diâmetro muito pequeno são esticados cruzando ambo
Ar forçado a 25 °C e 10 m/s é usado para resfriar componentes eletrônicos montados sobre uma placa de circuito impresso. Considere um chip com 4 mm de comprimento e 4 mm de largura, localizado a 120 m