Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 42
Considere uma célula a combustível delgada com 50 mm × 50 mm similar a do Exemplo 1.5, com ar em escoamento paralelo sobre suas superfícies. Fios com diâmetro muito pequeno são esticados cruzando ambos os lados da célula a uma distância x = da aresta frontal da célula para tornar o escoamento turbulento. Usando uma correlação apropriada deste capítulo, determine a velocidade mínima requerida para manter a temperatura da célula a combustível a = 77 °C e a posição correspondente do fio. O ar e a vizinhança da célula estão a = = 27 °C e a célula dissipa = 11 W. A emissividade da célula é ε = 0,85.
Passo 1
Tá legal! Nesse exercício, a primeira coisa que devemos perceber é que toda a energia gerada na célula será perdida para o ambiente, uma parte por convecção e outra por radiação, então, podemos escrever:
E, como o enunciado nos disse que temos escoamento em ambas as superfícies da placa, podemos escrever as equação para o calor por convecção e radiação da seguinte forma:
Agora, podemos isolar o coeficiente convectivo médio dessa equação obtendo:
E, substituindo os valores conhecidos, chegamos em:
Passo 2
Agora, como no nosso caso temos camada limite mista, vamos utilizar a equação 7.38 vista nesse capítulo para o número de Nusselt, que será dado por:
E, da equação 7.39 temos a expressão para A:
Dessa forma, substituindo essa expressão na equação acima, teremos:
Agora, sabendo que a equação para o número de Reynolds é dada por:
Vamos precisar das propriedades do ar. Nesse exercício vamos considerar . Então, para essa temperatura, temos as seguintes propriedades para o ar:
Então, calculando o valor de Reynolds na posição x = L, temos:
E, para o Reynolds crítico, podemos deixar em função do comprimento crítico, então, teremos:
Passo 3
Agora, sabendo que podemos escrever o coeficiente convectivo em função do número de Nusselt da seguinte forma:
Então, substituindo a expressão descrita no passo 2 para Nusselt, temos:
E, agora, substituindo as expressões calculadas para Reynolds, temos:
Então, nessa equação temos somente duas incógnitas, e , então, plotando o gráfico da velocidade em função do comprimento crítico, que é dado pela posição do fio, teremos:
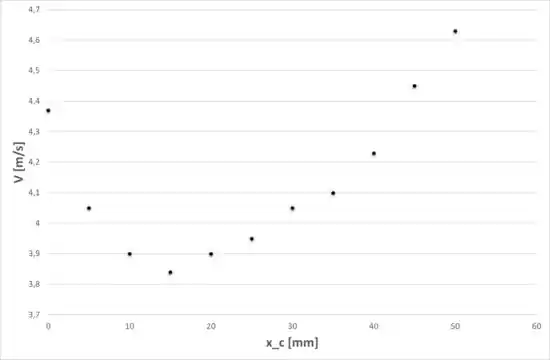
Então, através do gráfico podemos admitir que a velocidade mínima para manter a temperatura da célula a combustível a 77 °C é:
E a posição correspondente do fio, ou seja, o comprimento crítico, será: