Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 131

Uma seção de teste de um túnel de água tem 1 m de diâmetro e as propriedades do escoamento são V = 20   m / s , p = 100   k P a e T = 20 ° C . O bloqueio da camada limite no final da seção é 9%. Se um difusor cônico for adicionado ao final da seção para alcançar a máxima recuperação de pressão, qual será o ângulo, o comprimento, o diâmetro e a pressão de saída para recuperação máxima?

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.

ρ = 998   k g / m ³

μ = 0,001   k g / m . s

O número de Reynold é bem alto nesse nosso sistema, se liga!

R e = ρ V t D μ = 998 20 1 0,001 = 2   x   10 7

Passo 2

O bloqueio B e = 9 % = 0,09 a tabela 6.6 do livro nos mostra que C p m á x = 0,71

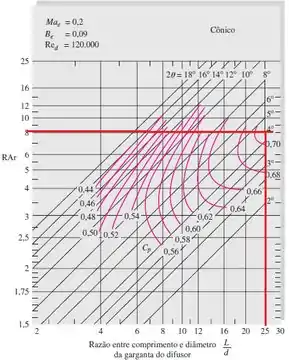
Olhando no gráfico para uma curva hipotética de C P m á x = 0,71 temos um L D ≈ 25 e 2 θ ≈ 4 °   e A R ≈ 8 .

Passo 3

Ou seja, vamos ter que θ = 2 °

L D ≈ 25 → L ≈ 25 D ≈ 25   m

O diâmetro de saída possui uma relação com o diâmetro do túnel:

D s a í d a = D A R 1 2 = 2,8   m

Passo 4

Podemos de igual maneira calcular o valor de C p relacionado com a diferença de pressão no túnel com a pressão de saída:

C P = P s a i d a - P t 1 2 ρ V t 2 = 0,71 = P s a í d a - 100000 1 2 998 20 2 → P s a í d a = 242000   P a

Resposta

θ = 2 °

L = 25   m

D s a í d a = 2,8   m

P s a í d a = 242   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 8—68 supondo que (a) o diâmetro do tubo seja o dobro e (b) o comprimento do tubo seja o dobro.
Óleo a 20 0 C escoa através de um funil de vidro vertical que consiste em um reservatório cilíndrico de 15 cm de altura e um tubo de 1 cm de diâmetro e 25 cm de altura. O funil sempre é mantido cheio
Um tanque de 3 m de diâmetro está inicialmente cheio com água até 2 m acima do centro de um orifício com diâmetro de 10 cm e aresta viva. A superfície da água do tanque é aberta para a atmosfera e o o
Um tanque de 3 m de diâmetro está inicialmente cheio com água até 2 m acima do centro de um orifício com diâmetro de 10 cm e aresta viva. A superfície da água do tanque é aberta para a atmosfera e o o
Um tanque de água cheio com água aquecida por aquecimento solar a 40 0 C deve ser usada para banhos de chuveiro em um acampamento usando o escoamento por gravidade. O sistema inclui 20 m de tubulação