Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 71
Um tanque de água cheio com água aquecida por aquecimento solar a deve ser usada para banhos de chuveiro em um acampamento usando o escoamento por gravidade. O sistema inclui 20 m de tubulação de ferro galvanizado de 1,5 cm de diâmetro com quatro curvas chanfradas ( ) sem aletas e uma válvula de globo totalmente aberta. Se a água deve escoar a uma taxa de 0,7 L/s através do chuveiro, determine qual deve ser a altura do nível da água no tanque com relação ao nível de saída do chuveiro. Despreze as perdas na entrada e no chuveiro, e despreze o efeito do fator de correção da energia cinética
Passo 1
Oi pessoal, tudo bem?
Primeiramente, para o problema, assumimos que:
1. O fluxo é constante e incompressível.
2. Os efeitos de entrada são insignificantes e, portanto, o fluxo é totalmente desenvolvido.
3. O fluxo é turbulento, de modo que o valor tabulado dos coeficientes de perda possa ser usado (a ser verificado).
4. O a diferença de altitude entre a superfície livre de água no tanque e o chuveiro permanece constante.
5. Não há bombas ou turbinas no sistema de tubulação.
6. As perdas na entrada e no chuveiro são consideradas insignificantes.
7. O tanque de água está aberto para a atmosfera.
8 O efeito do fator de correção da energia cinética é desprezível, α = 1.
Do problema, temos:
Obs: propriedades da água à , Tabela A.3 do livro.
Passo 2
Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:
E tomamos o ponto 1 na superfície livre do reservatório e o ponto 2 na saída do tubo, que também é considerado o nível de referência (), conforme o esboço a seguir:
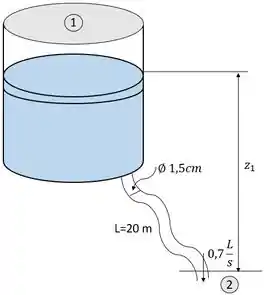
O sistema de tubulação envolve 20 m de tubulação de 1,5 cm de diâmetro, uma entrada com perda insignificante, 4 curvas em meia esquadria (90 °) sem palhetas ( cada) e uma válvula globo aberta ().
O líquido em ambos os pontos é aberto para a atmosfera (e, portanto, ), o nível de fluido no reservatório é constante (). Então a equação de energia para um volume de controle entre esses dois pontos simplifica a:
Onde a perda de carga é encontrada pela equação da perda de carga menor somado com a perda de carga maior, assim:
Passo 3
A velocidade, o número de Reynolds, e o fator de atrito em cada tubo são expressos como:
Agora, o número de Reynolds é expresso:
E o fator de atrito é expresso como:
Resolvendo de forma iterativa (ferramenta Solve, do Excel), encontramos .
Passo 4
Observe que não consideramos a perda de saída, a menos que a velocidade de saída seja dissipada dentro do sistema considerado (neste caso, não é). Então, a perda total de carga e a elevação da fonte se tornam:
E por fim, substituindo os valores na equação 2:
Obs: Os números de Reynolds respectivos estão na ordem de , portanto a verificação se o regime é turbulento foi realizada.
Resposta
Portanto: