Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 133

Uma seção de teste de um túnel de vento tem seção quadrada de 91 cm de lado com as seguintes propriedades de escoamento: V = 45,7   m / s , pressão absoluta p = 103,4   k P a e T = 20 ° C . O bloqueio da camada limite ao final da seção de teste é 8%. Determine o ângulo, o comprimento, a altura e a pressão de saída de um difusor de paredes planas adicionado à seção de teste para alcançar a máxima recuperação de pressão.

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades do ar.

ρ = 1,2   k g / m ³

μ = 1,8   x   10 - 5   k g / m . s

Vamos calcular o Reynold desse paranauê?

R e = ρ V D μ = 1,2 45,7 0,91 1,8   x   10 - 5 = 2,7   x 10 6

Note que esse valor é muito acima do valor da figura 6.28ª do livro, mas ainda assim vamos ter que apelar pra essa figura porque é o que temos pra hoje hehe

Passo 2

Bem, considerando um bloqueio de 8%, ou seja, 0,08 a tabela abaixo nos mostra que para paredes planas, temos que C P m á x = 0,7

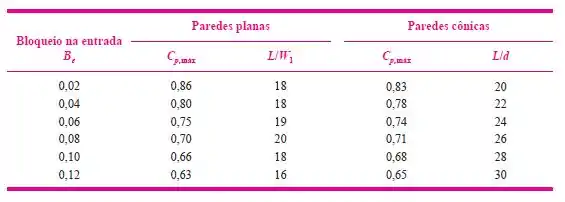
Passo 3

De posso deste valor de C P m á x vamos no gráfico de difusor de paredes planas e vamos observar que:

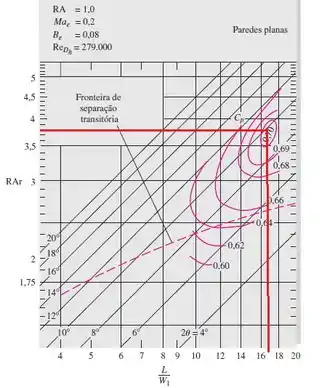
Temos um valor aproximadamente de:

L W 1 = 17

2 θ = 9,5 °

A R = 3,75

Passo 4

Com isso podemos dizer que:

θ = 4,75 °

L 1 = 17 W 1 = 17 0,91 = 15,47   m

W 2 = A R W 1 = 3,75 0,91 = 3,41   m

C P = P s a i d a - P t 1 2 ρ V t 2 → P s a í d a - 103400 1 2 1,2 45,7 2 = 0,7 → P s a í d a = 104379

Resposta

θ = 4,75 °

L 1 = 17 W 1 = 17 0,91 = 15,47   m

W 2 = A R W 1 = 3,75 0,91 = 3,41   m

P s a í d a = 104379

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trocador de calor consiste em passagens múltiplas entre placas planas paralelas, como mostra a Figura P6.97. A queda de pressão disponível é de 2 kPa e o fluido é água a 20 ° C. Se a vazão total de
Um túnel de vento de madeira tem 28 m de comprimento e uma seção retangular de 50 cm por 80 cm. Por meio de um ventilador, o túnel aspira ar em condição padrão ao nível do mar. Se o ventilador fornece
Repita o Problema 6.92 incluindo as perdas localizadas causadas pela entrada em canto vivo, pela saída para a sala e por uma válvula de gaveta aberta. Se a pressão na sala é um vácuo de 10 Pa, em que
Trocadores de calor consistem frequentemente em muitas passagens triangulares. Uma passagem é mostrada na Figura P6.91, com L = 60 cm e seção transversal em formato de um triângulo isósceles de compri
Um tubo de chapa de aço de 27,4 m de comprimento transporta ar a aproximadamente 20 ° C e 1 atm. A seção transversal do tubo é um triângulo equilátero cujo lado mede 229 mm. Se um ventilador pode forn