Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 91

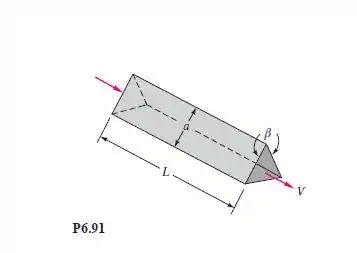
Trocadores de calor consistem frequentemente em muitas passagens triangulares. Uma passagem é mostrada na Figura P6.91, com L = 60 cm e seção transversal em formato de um triângulo isósceles de comprimento lateral a = 2 cm e ângulo b = 80 ° . Se a velocidade média é V = 2 m/s e o fluido é óleo SAE 10 a 20 ° C, calcule a queda de pressão.

Passo 1

Bora pra mais uma!

Para o óleo SAE 10 ρ = 870 k g m 3 ; μ =   0,104 k g m s .

Calculando o número de Reynolds com base no comprimento do lado a, obtemos:

R e = ρ V a μ = 870 k g m 3 0,104 k g m s * 0.02 m * 2 m s = 334,62   ( R e g i m e   l a m i n a r )

Como o triangulo é isósceles, a parte de baixo medirá 2 * 0,02 m * s e n 40 ° = 0,024 m . Podemos então calcular o diâmetro hidráulico desta tubulação:

D h = 4 A P

A = 1 2 * 0,024 m * 0,02 m c o s 40 ° = 1,94 * 10 - 4 m ²

P = 0,0657 m

D h = 0,012 m

Agora, podemos calcular o número de Reynolds:

R e = ρ V D h u = 870 k g m 3 0,104 k g m s * 0.012 m * 2 m s = 200,77

Da tabela 6.4 do livro, para um ângulo de 40 ° temos que f R e D h = 52,9 → f = 0,263 .

Agora, vamos calcular a queda de pressão:

∆ P = f L D h * ρ 2 V 2 = 0,263 * 0,6 m 0,012 m * 870 k g m 3 2 * 4 m 2 s 2 = 23000 P a

Resposta

A queda de pressão é de 23000 Pa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um escoamento completamente desenvolvido em um tubo cilíndrico de raio R e comprimento L = 10m m , com o escoamento gerado pela aplicação de um gradiente de pressão Δ p . Testes foram realiz
O experimento “pitchdrop” (piche em queda) vem sendo repetido continuamente na Universidade de Queensland desde 1927 (http://www.physics.uq.edu.au/physics_museum/pitchdrop.shtml). Neste experimento, u
No esquema da figura, o nível da água é mantido constante. Determinar:O coeficiente de velocidade;O número de Reynolds teórico;O tempo que a água levará para subir 10c m ao fechar o registro do bocal;
Num trecho de conduto retangular 20c m × 40c m para ventilação, escoa ar ( ρ = 1,2k g / m 3 ) , considerado incompressível, com uma vazão de 2m 3 / s . Determinar:O coeficiente de perda de carga singu
Uma sala de 4m × 6m × 3m é usada como cabine de pintura. Sabe-se que numa cabine de pintura o ar ( ρ = 1,2k g / m 3( c o n s t a n t e ) ; v = 10 - 5m 2 / s ) deve ser trocado, por norma, no mínimo 60