Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 101
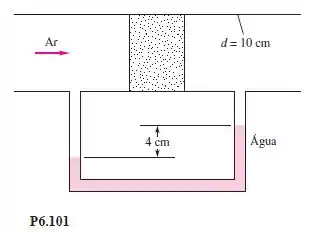
A Figura P6.101 mostra um ensaio de perdas para um filtro espesso. A vazão no tubo é de 7 m³/min e a pressão a montante é de 120 kPa. O fluido é o ar a 20C. Usando a leitura do manômetro de coluna de água, estime o coeficiente de perda K do filtro.
Passo 1
Bora pra mais uma!
A densidade da corrente de ar é:
Agora, vamos calcular a velocidade média no tubo para relacionarmos com o coeficiente de perda K:
A diferença de pressão do manômetro será:
Por fim, relacionaremos K com a diferença de pressão do manômetro e com a velocidade:
Resposta
O coeficiente de perda do filtro vale aproximadamente 2,5.
Exercícios de Livros Relacionados
O perfil de velocidade para escoamento completamente desenvolvido de óleo castor a 20 °C entre placas paralelas em movimento, é dado pela Eq. 8.8. Considere U = 1,5m / s e a = 5m m . Determine o gradi
O perfil de velocidade para escoamento completamente desenvolvido de tetracloreto de carbono a 15 °C entre placas paralelas (espaçamento a = 1,25m m ), com a placa superior em movimento, é dado pela E
Glicerina a 15 °C escoa entre placas paralelas com espaçamento b = 2,5m m entre elas. A placa superior move com velocidade U = 0,6m / s no sentido positivo de x . O gradiente de pressão é ∂ p / ∂ x =
Um inventor propõe fabricar um “cronômetro viscoso” colocando um cilindro pesado dentro de outro cilindro ligeiramente maior contendo um líquido viscoso, formando assim uma película anular delgada ent
Uma película de tinta molhada de espessura uniforme, δ , está pintada sobre uma parede vertical. A tinta molhada pode ser aproximada como um fluido de Bingham com tensão de escoamento τ y e massa espe