Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 55
As temperaturas (em K), em regime estacionário, de três pontos nodais de uma longa barra retangular são fornecidas na figura. A barra experimenta uma taxa de geração volumétrica de calor uniforme igual a e tem uma condutividade térmica de Dois de seus lados são mantidos a uma temperatura constante de 300 K, enquanto os demais se encontram isolados.
- Determine as temperaturas nos nós 1, 2 e 3.
- Calcule a taxa de transferência de calor saindo da barra, por unidade de comprimento , utilizando as temperaturas nodais. Compare esse resultado com o da taxa calculada a partir do conhecimento da taxa de geração volumétrica e das dimensões da barra.
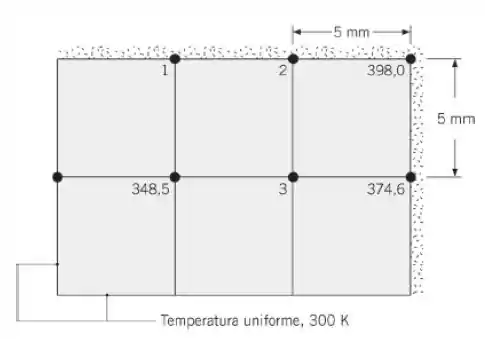
Passo 1
Boom galerinha, mesmo esquema das demais certo?
Mas aqui nós vamos dividir a barra de uma forma um pouco diferente do que o problema nos mostrou, com calores sendo perdido para o ambiente em cada quadradinho:
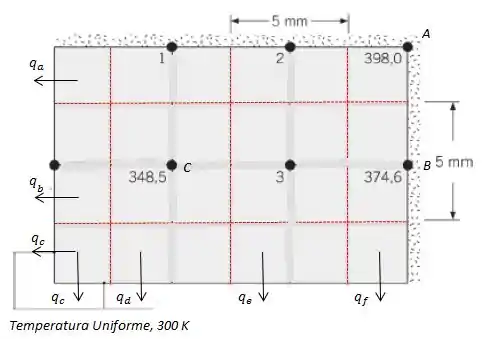
Como todos os nós são interiores nós podemos usar a seguinte equação:
Como
Substituindo:
Se olharmos o nó A e lembrando da simetria:
Substituindo as temperaturas:
Passo 2
Se usarmos agora o nó de número 3:
Substituindo:
E para o nó 1:
Substituindo:
E assim nós finalizamos a letra (a) !!
Passo 3
Boom, agora a taxa de calor que entra na barra é calculada pela taxa de calor que volume de controle, nas paredes com temperatura uniforme, mais a energia gerada:
Se a energia é dada por:
Então:
Substituindo:
E acabamos mais uma galerinhaa !!