Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 34

Seja o transformador do Problema 8.103, cuja superfície lateral está sendo mantida a 47 ° C por uma linha de refrigerante por convecção forçada que remove 1000   W . Deseja-se estudar o resfriamento do transformador por convecção natural e radiação, admitindo que a superfície tem uma emissividade de 0,80 .

  1. Determine a potência que pode ser removida por convecção natural e radiação nas superfícies lateral e na superfície horizontal superior, quando as temperaturas ambiente e da vizinhança são de 27 ° C .

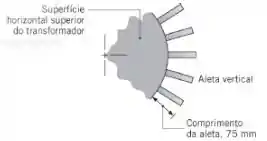
(b) Aletas verticais, com   5   m m de espessura, 75   m m de comprimento e 500   m m de altura, podem ser facilmente soldadas à superfície lateral. Qual é a taxa de remoção de calor por convecção natural se 30 dessas aletas forem fixadas ao transformador?

Passo 1

Fala aiii, vamos resolver uma questão de placas horizontais e planos inclinados?! Aqui nós temos um transformador que dissipa 1000   W cuja superfície deve ser mantida a 47 ° C em ar inativo e arredores a 27 ° C .

Com isso queremos encontrar a remoção de energia por convecção livre e radiação das superfícies horizontais laterais e superiores e com 30 aletas verticais ligadas à superfície lateral, beleza?

Passo 2

Para resolver essa questão vamos assumir:

(1) As aletas são isotérmicas à temperatura da superfície lateral, T s ;

(2) Aletas verticais e superfície lateral se comportam como placas verticais;

(3) O transformador possui superfícies isotérmicas e perde calor apenas na parte superior e lateral.

Para as superfícies vertical lateral ( l a t ) e horizontal superior ( t o p ) , a perda de calor por radiação e convecção é,

q = q l a t + q t o p = h - l a t + h r ( π D L ) T s - T ∞ + h - t o p + h r π 2 D 4 ( T s - T ∞ )

Onde o coeficiente de radiação linearizado é,

h r = ε σ ( T s + T ∞ ) ( T s 2 + T ∞ 2 )

h r = 0,2 8 × 5,67 × 10 - 8 W m 2 . K 4 320 + 300 K 320 2 + 300 2 K 2 = 5,41 W m 2 . K

Passo 3

O coeficiente de convecção livre para as superfícies lateral e superior é:

Placa lateral-vertical:

R a L = g β ( T s - T ∞ )   H 3 ν α = 9,8 m s 2 1 / 310 K 47 - 27 K 0,5 m 3 1 6,90 × 10 - 6 m 2 s 2 3,98 × 10 - 6 m 2 s = 1,950 × 10 8

E,

N u L - = 0,825 + 0,387   1,950 × 10 8 1 6 1 + 0,492 0,7 06 9 16 8 27 2 = 74,5

h - = N u L - k H = 74,5 × 0,02 7 W m . K 0,5 m = 4,0 2 W m 2 . K

Passo 4

Placa superior horizontal:

L c = A s P = π D 2 / 4 π D = D 4 = 0,0575 m

R a L = g β ( T s - T ∞ )   H 3 ν α = 9,8 m s 2 1 / 310 K 47 - 27 K 0,0575 m 3 16,90 × 10 - 6 m 2 s 23,98 × 10 - 6 m 2 s = 2,97 × 10 5

E,

N u L - = 0,54   R a L 1 4 = 0,54 2,97 × 10 5 1 4 = 12,6  

h t o p - = N u L - k L c = 12,6 × 0,027 W m . K 0,0575 m = 5,92 W m 2 . K

Portanto, a perda de calor por convecção e radiação é:

q = 72,7   W

Passo 5

O efeito da adição das aletas verticais é aumentar a área da superfície lateral para,

A w f = π D H - 30 t × H + 30 × 2 ( w × H )

A w f = π 0,23 m × 0,50 m - 30 0,005 m × 0,500 m + 30 × 2 ( 0,075 m × 0,500 m )

A w f = 2,536   m 2

Onde t e   w são a espessura e a largura das aletas, respectivamente. Portanto, a perda de calor é agora,

q = q l a t + q t o p = h - l a t + h r A w f T s - T ∞ + q t o p

Ou seja,

q = 483   W

Resposta

  1. q = 72,7   W
  2. q = 483   W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o aquecedor elétrico do Problema 7.49. Se o soprador apresentar defeito, interrompendo o escoamento do ar enquanto o aquecedor continua operando a 1000W / m , qual temperatura o aquecedor ir
Um aquecedor de ar por convecção natural é constituído por uma série de placas verticais paralelas igualmente espaçadas, que podem ser mantidas a uma temperatura fixa T s por aquecedores elétricos nel
A porta frontal de um lava-louças, com largura de 580m m , tem um respiradouro de ar vertical com 500m m de altura que apresenta um espaçamento de 20m m entre a bacia interna, que opera a 52 ° C , e u
A chapa de vidro da janela de um edifício, que tem 1,2 m de altura por 0,8 m de largura, é protegida do ambiente externo por uma outra janela (contra tempestades) com as mesmas altura e largura. O esp
Uma série de placas de circuitos verticais encontra-se imersa em ar ambiente quiescente a T ∞ =17 ° C . Embora os componentes sejam salientes em relação aos substratos, é razoável, em uma primeira apr