Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 29
Uma série de chips eletrônicos é montada no interior de um recipiente retangular fechado e o resfriamento é implementado pela fixação de um dissipador de calor de alumínio . A base de um dissipador tem dimensões de , enquanto as 6 aletas têm espessura e passo . O comprimento das aletas é de e a base do dissipador de calor tem uma espessura de .
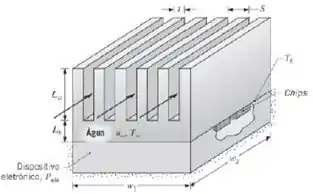
Se o resfriamento é promovido pelo escoamento de água através do dissipador de calor com e , qual é a temperatura da base do dissipador quando a potência dissipada pelos chips for de ? O coeficiente convectivo médio nas superfícies das aletas e na base exposta pode ser determinado supondo escoamento paralelo sobre uma placa plana. As propriedades da água podem ser aproximadas por , , , e .
Passo 1
Eita! Temos um problema que envolve dissipação de calor com aletas!! Chega já começa a assustar!
Mas calma, vamos com calma que iremos conseguir resolver ela tranquilamente. Calma é a resposta para o sucesso!
Vamos entender o que acontece com o problema. Temos chips que estão gerando calor , o qual está sendo dissipado pelas aletas. O objetivo desta questão será determinar a temperatura da base de alumínio. Mas, para isto, precisamos determinar alguns pontos.
Como ocorre essa dissipação? Vamos tentar associar as fontes por resistências térmicas e utilizar a metodologia estudada lá na parte de condução unidimensional.
Bom, então, ele será dissipado pelas aletas por convecção. Em termos de resistência térmica, temos a seguinte relação:
Eita. São tantos termos que assusta ainda mais. Não se assustem, vamos discutir um pouco mais sobre eles a frente. Então, continuando, já sabemos que o calor será dissipado pelas aletas. Mas como eles chegaram as aletas? Isto ocorrerá por condução da base. Em termos de
resistência, temos:
Portanto, podemos escrever a seguinte equação para a taxa de transferência de calor:
E esta é a relação que devemos utilizar para determinar a temperatura da base.
Passo 2
Vamos destrinchar agora a relação das aletas. Relembrando, temos a seguinte equação para a sua resistência térmica:
Agora, vamos entender cada um dos termos. A constante corresponde ao número de aletas. Portanto, . A constante é a área superficial das aletas em contato com o ar. Portanto, ele será expresso por:
E quem é a constante ? É a soma da área superficial de todas as aletas com a área da base em contato com o ar. Portanto,
E o termo ? Ela é a eficiência da aleta. Considerando que temos uma aleta plana retangular, a relação correta é . Mas, para calcularmos, vamos precisar do coeficiente de transferência de calor (e também é uma das constantes da fórmula de resistência térmica).
Como a questão já nos disse para assumir escoamento laminar na superfície das aletas, não precisamos nos preocupar com qual a relação devemos obter para o número de Nusselt (e consequentemente, para o coeficiente). Então, a relação que devemos utilizar é:
Calculando o número de Reynolds, temos:
Portanto, o coeficiente de transferência de calor será:
Pronto! Agora, realmente só falta a eficiência . Calculando o coeficiente , temos:
E o comprimento característico . Portanto,
Então, a resistência térmica será:
Muito trabalho né? Percebam que não são contas “muito difíceis”. O que confunde é a quantidade de relações que devemos utilizar.
Passo 3
Agora já temos todas as informações necessárias para obter a temperatura da base. Lembrando da relação e reorganizando, temos:
Então,
E esta é a resposta da questão.