Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 32
Uma fita de aço emerge da seção de laminação a quente de uma usina siderúrgica a uma velocidade de e a uma temperatura de 1200 K. Seu comprimento e espessura são e , respectivamente, e a sua densidade e calor específico são e , respectivamente.
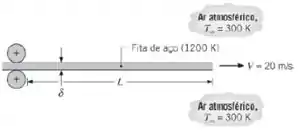
Levando em consideração a transferência de calor nas superfícies superior e inferior da fita, e desprezando efeitos da radiação e da condução na fita, determine a taxa de variação com o tempo da temperatura da fita a uma distância de 1 m da aresta frontal e na aresta de saída. Determine a distância da aresta frontal onde ocorre a taxa de resfriamento mínima.
Passo 1
Precisamos determinar a taxa de variação da temperatura no tempo sob duas condições distintas e a distância da aresta frontal onde ocorre a taxa de resfriamento mínima. Este segundo ponto vocês vão perceber que é mais simples de calcular, é só saber aonde que ele é.
Agora, a taxa de variação da temperatura no tempo é um pouco mais complicado. Mas também não é nada de outro mundo. Nós vamos precisar fazer um balanço de energia.
E, para isto, vamos partir de elementos diferenciais. Ajuda bastante fazermos um simples esboço, como o esboço abaixo, para ajudar a gente na hora de elaborar os termos. Considerando o volume de controle se movendo com a fita, temos:
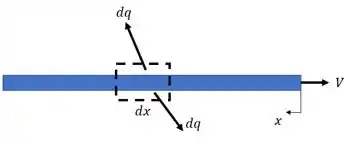
Se a gente considera o volume de controle se movendo, não temos nenhuma energia entrando nem sendo gerada. Apenas temos os termos de energia que sai e o termo de energia acumulada. Portanto, temos o seguinte balanço:
Passo 2
Agora, quem é o termo que sai e o de energia acumulada? O termo que sai é o (cuidado com o 2, pois temos a superfície superior e inferior), e ele é devido a ação da convecção. Então,
E o termo de energia acumulada? Ele é dado por:
Portanto, o nosso balanço de energia é:
E esta equação corresponde a taxa de variação da temperatura no tempo!
Passo 3
Agora precisamos utilizar a taxa de variação descoberta no final do Passo 2 para calcularmos dois casos particulares e . Mas, antes disto, vamos facilitar nossa vida!
Sempre que possível isto é muito bom! Vamos substituir os valores das constantes do aço. Como a questão já nos deu os valores, não precisamos ir em tabela nenhuma para resolver.
Substituindo os valores, temos:
Agora, precisamos do para cada caso. Mas, para isto, vamos precisar das propriedades do ar, o qual está em 1 atm e tem temperatura do filme igual a . Então, utilizando a tabela , temos: , , .
De uma forma geral, os dois casos tem o mesmo procedimento. Primeiro calculamos o número de Reynolds e checamos se é laminar ou turbulento. Depois, escolhemos a correlação correta para o número de Nusselt. Por fim, correlacionamos com o coeficiente .
Confuso? É não! Vamos ver devagar então! Começando por , temos:
Como , temos o caso de escoamento laminar. Portanto, a correlação correta para o número de é:
Assim, a taxa de variação da temperatura é:
Agora, vamos repetir todo o procedimento para .
Como , temos o caso de escoamento turbulento. Portanto, a correlação correta para o número de é:
Assim, a taxa de variação da temperatura é:
Passo 4
Para finalizarmos a questão, temos que determinar a distância da aresta frontal onde ocorre a taxa de resfriamento mínima.
E agora? Aonde será que ocorre esta distância mínima? Esta pergunta que é a dificuldade deste cálculo. Se nós soubermos que ele fica logo antes da transição laminar/turbulento (pode imaginar em cima da transição), vamos saber resolver fácil.
Agora que sabemos aonde que é, e também sabemos que na transição temos , é só descobrir qual o valor de que satisfaz essa relação. Portanto,
E esta é a distância da aresta frontal até o ponto de mínima taxa de resfriamento.
Resposta
Para , temos a seguinte taxa:
Já para , temos:
A distância da aresta frontal até onde ocorre a taxa de resfriamento mínima é: