Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 3
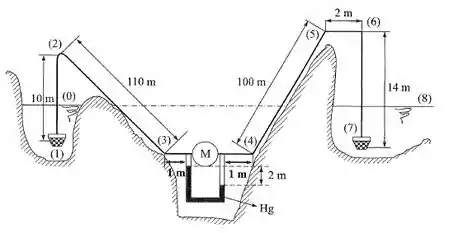
No sistema esquematizado, conhece-se e sabe-se que o sentido de escoamento é de (0) para (8). Com os dados da figura, determinar:
a) a energia por unidade de peso trocada entre a máquina e o fluido e o tipo de máquina;
b) o coeficiente de perda de carga distribuída.
Dados: ; ; .
Passo 1
Beleza, a primeira coisa é notar que a máquina do problema é uma bomba, pois através do manômetro da figura, podemos ver que a pressão de saída é maior que a de entrada, característica desse tipo de máquina. Agora sabemos que a carga da bomba é a diferença entre a carga de saída e de entrada da mesma, então:
Para encontrar a diferença entre a pressão de saída e de entrada, podemos aplicar o equilíbrio manométrico para o manômetro instalado na bomba, então temos:
Substituindo os valores conhecidos:
Agora, voltando a equação para a carga da bomba, temos:
Passo 2
Agora vamos aplicar o equilíbrio de energia entre os pontos 0 e 8
Substituindo os valores conhecidos:
Agora precisamos escrever a fórmula para a perda de carga no sistema, que será dada por:
Onde representa a perda de carga ao longo da tubulação e o termo representa as perdas localizadas. Nesse caso, temos os valores das perdas localizadas, então:
Agora precisamos encontrar a velocidade do escoamento, como temos a vazão e o diâmetro da tubulação, ficou fácil:
Agora podemos calcular o termo que representa a perda localizada:
Passo 3
Agora retornando para a equação da perda de carga no sistema apresentada no passo 2:
Substituindo os termos que já foram encontrados:
E, sabemos que a fórmula para a perda de carga distribuída é dada por:
Como temos uma seção circular, então , então, isolando e substituindo os valores conhecidos: