Na instalação são dados: reservatório de grandes dimensões; ; .
Determinar:
a) a vazão em volume;
b) a perda de carga na instalação;
c) o valor de x;
d) substituindo o cotovelo (2) por uma turbina e mantidas as demais condições, determinar sua potência, sabendo que .
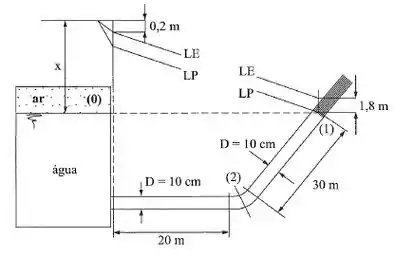
Passo 1
Tá legal, vamos começar o exercício lembrando que a diferença entre a linha de energia e a linha piezométrica corresponde à parcela cinética do escoamento, então podemos escrever:
Substituindo a altura dada no diagrama do enunciado, temos:
Agora com esse valor, podemos encontrar a vazão no sistema:
Passo 2
Agora para a letra b), vamos aplicar a equação da perda de carga para o sistema entre os pontos 0 e 1, então podemos escrever:
Onde é a perda de carga na saída do reservatório, nesse caso não precisamos nem fazer conta, pois a diferença entre e a linha de energia já indica a perda de carga, então temos:
Agora para encontrar precisamos aplicar a equação para a perda de carga localizada, que é dada por:
E a perda de carga distribuída é calculada através de:
Substituindo os valores conhecidos, temos:
Então, voltando à equação da perda de carga escrita no começo desse passo e substituindo os valores conhecidos, temos:
Passo 3
Agora para descobrir o valor da altura pedido na letra c), vamos aplicar o equilíbrio de energia entre os pontos 0 e 1, então:
Substituindo os valores conhecidos:
Só que nós sabemos que o termo representa a altura de carga no ponto 0, que é justamente o valor de , já que ele indica a altura da energia do sistema naquele ponto, então:
Passo 4
Agora para descobrir a potência de uma bomba instalada em (2), precisamos primeiro determinar sua carga, e faremos isso aplicando o equilíbrio de energia entre os pontos 0 e 1:
Substituindo os valores conhecidos (lembrando que agora não temos perda localizada em (2) como tínhamos nos passos anteriores:
Agora, substituindo esse valor na equação para potência de uma turbina, temos: