Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 14.Problemas - Ex. 40

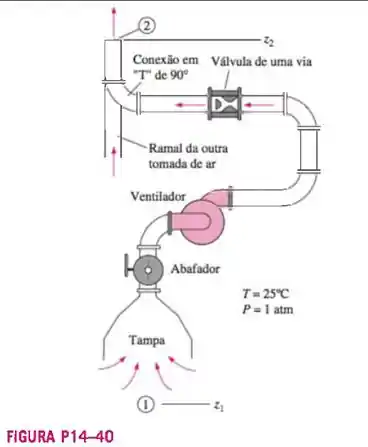
Um sistema de ventilação local (sistema de tampa e duto) é usado para remover o ar e os contaminantes produzidos por um laboratório farmacêutico (Figura 14-40). O diâmetro

interno ( D I ) do duto é D   = 150   m m , sua rugosidade média é de 0,15   m m e seu comprimento total é L   = 24,5   m . Existem três cotovelos ao longo do duto, cada um com um coeficiente de perda menor de 0,21 . A literatura do fabricante relaciona o coeficiente de perda na entrada da tampa como 3,3 com base na velocidade do duto. Quando o abafador está totalmente abertoseu coeficiente de perda é de 1,8 . O coeficiente de perda menor através do tê de 90° é 0,36 . Finalmente, uma válvula de uma via é instalada para evitar que os contaminantes de uma segunda tampa escoam “de volta” para a sala. O coeficiente de perda menor da válvula de uma via (aberta) é 6,6 . Os dados de desempenho do ventilador se ajustam a uma curva parabólica com a forma H d i s p o n í v e l = H o - a V ˙ 2 , na qual a carga de fechamento H 0 =   60,0   m m de coluna de água, o coeficiente a =   2,50   X   10 - 7   m m de coluna d’água por L p m 2 , a carga disponível H d i p o n í v e l esta em unidade de m m de coluna d’água e a capacidade está em unidades de L p m de ar. Estime a vazão em L p m em todo o sistema de ventilação.

Passo 1

Opaaa! Vamos nessa pra uma questãozinha de ventiladores!!!

O problema da um TEXTÃO pra a gente, mas relaxa..vamos devagarinho!

Começando pela equação de energia:

H r e q u e r i d o = P 2 - P 1 ρ h + V 2 2 2 g + z 2 - z 1 + h L , t o t a l

A figura marca os pontos 1 e 2 , ambos estão na pressão atmosférica, então podemos cancelar esse termo! O diâmetro da saída é muito maior do que o de entrada, logo a gente pode desconsiderar a velocidade de saída e por fim...a diferença de altura pra gases influencia muito pouco, então podemos cortar esse termo também, ficamos com:

H r e q u e r i d o = V 2 2 2 g + h L , t o t a l

A perda de carga é dada por:

h L , t o t a l = f L D   + ∑ K L V 2 2 g

Substituindo, chegamos em:

H r e q u e r i d o = V 2 2 2 g + f L D   + ∑ K L V 2 2 g

Passo 2

O problema nos da a equação do H d i s p o n í v e l :

H d i s p o n í v e l = H o - a V ˙ 2

E nos da também:

H 0 =   60,0   m m   d e   c o l u n a   d e   á g u a

a =   2,50 ×   10 - 7   m m   d e   c o l u n a   d ’ á g u a   /   L p m 2

Aqui a gente vai ter que tomar cuidado!!! As unidades estão em mm de água, mas o nosso fluido é ar, para converter o H 0 fazemos:

H 0 , m m   d e   a r = H 0 , m m   d e   á g u a × ρ á g u a ρ a r

Para 25 ° C temos     ρ á g u a = 997 k g m 3 , ρ a r = 1,184 k g m 3   , substituindo:

H 0 , m m   d e   a r = 60,0   m m   d e   a r × 997 1,184 = 5,05 × 10 4   m m   d e   a r

Agora o a :

a =   2,50 ×   10 - 7   m m   d e   c o l u n a   d ’ á g u a   /   L p m 2

Fazemos:

a m m   a r / L P M 2 = a m m   á g u a / L P M 2 × ρ á g u a ρ a r

Substituindo:

a m m   a r / L P M 2 = 2,50   X   10 - 7   × 997 1,184 = 2,11 × 10 - 4 m m L p m

Passo 3

No ponto de operação temos:

H d i s p o n í v e l = H r e q u e r i d o

Então vamos substituir:

H o - a V ˙ 2 = V 2 2 2 g + f L D   + ∑ K L V 2 2 g

Vamos escrever tudo em termos de velocidade?! Bora então..a vazão é dada por:

V ˙ = π D 4 4 V

Substituindo:

H o - a π D 4 4 V 2 = V 2 2 2 g + f L D   + ∑ K L V 2 2 g

O problema nos da os seguintes dados:

H 0 = 5,05 × 10 4   m m   d e   a r

D = 150   m m

a = 2,11 × 10 - 4 m m L p m

L = 24,5   m

E o somatório de K L é dado pela soma de todas as perdas dadas pelo enunciado:

K L = 3 0,21 + 3,3 + 1,8 + 0,36 + 6,6 = 12,69   m

O problema é que não conhecemos f e ele depende da velocidade! Vamos precisar usar um método interativo então!!

Com isso achamos:

V = 6,71   m / s

Passo 4

Agora podemos calcular a vazão:

V ˙ = V π D 2 4

Substituindo os dados achamos:

V ˙ = 6,71 × π ( 150 × 10 - 3 ) 2 4 = 0,12   m 3 / s

Ou:

V ˙ = 7114   L p m

MEU DEUS, TA CERTO ISSO?!

Não se assusta, o valor é alto mas lembra que o nosso fluido é um gás, beleza?

Resposta

V ˙ = 7114   L p m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Figure 11.32 showed the typical power performance of awind turbine. The wind also causes a thrust force thatmust be resisted by the structure. The thrust coefficient CTof a wind turbine may be defi ne
The manufacturer of the wind turbine in the chapteropener photo claims that it develops exactly 100 kW at awind speed of 15 m/s. Compare this with an estimate fromthe correlations in Fig. 11.32.
To avoid the bulky tower and impeller and generator inthe HAWT of the chapter-opener photo, we could insteadbuild a number of Darrieus turbines of height 4 m anddiameter 3 m. (a) How many of these wou
The pump of Prob. P11.35 has a maximum efficiency of88percent at 8000 gal/min. (a) Can we use this pump, atthe same diameter but a different speed, to generate a BEPhead of 150 ft and a BEP fl ow rate
A Pelton wheel of 12-ft pitch diameter operates under a nethead of 2000 ft. Estimate the speed, power output, and flowrate for best effi ciency if the nozzle exit diameter is 4 in