Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 23

Para a situação descrita no Exemplo 6.4, a camada-limite pode ser levada ao estado turbulento pela aplicação de rugosidades na superfície da placa plana em uma posição específica x. Desta maneira, o local no qual ocorre a transição, xc, pode ser movido para uma posição a montante em relação à posição de transição associada a placa plana lisa do exemplo. Calcule e represente graficamente o coeficiente convectivo médio sobre toda a placa para a rugosidade sendo aplicada ao longo da faixa 0 ≤ xr ≤ L. Quais valores de xr fornecem os valores mínimo e máximo de h? Suponha a temperatura da água igual a 300 K.

Passo 1

Vamo analisar o enunciado junto pra entender o que ele quer de você.

A gente tem que voltar ao Exemplo 6.4. Temos aqui água escoando em uma placa lisa. Nessa questão agora, a gente vai analisar o problema caso tivesse rugosidade na placa, com um novo valor para a transição do regime laminar para o turbulento no ponto x r .

A placa tem comprimento L = 0,6   m e está a 300   K , onde o coeficiente de convecção h , somando as contribuições laminar e turbulenta, é dado pela equação:

h =   h l a m + h t u r b = 395 x - 0,5 + 2330 x - 0,2

Em primeiro lugar, devemos calcular o coeficiente de convecção médio h - , a partir da seguinte integral:

h - = 1 L ∫ 0 L h   d x  

Com essa integral, a gente vai deixar o coeficiente médio h - em função de x r , e no fim, vamos plotar um gráfico de h - por x r , e vamos encontrar os valores mínimo e máximo para a faixa 0 ≤ x r ≤ L.

Passo 2

Primeiro, a gente vai montar e resolver a integral.

Pra montar a integral de forma correta, devemos dividir ela em duas partes: uma antes do ponto crítico x r , onde o escoamento é laminar, e depois do ponto x r , onde o escoamento é turbulento.

Dessa forma, nossa integral, ao ser dividida em duas partes, fica assim:

h - = 1 L ∫ 0 x r h l a m   d x + ∫ x r L h t u r b   d x = 1 L ∫ 0 x r 395 x - 0,5   d x + ∫ x r L 2330 x - 0,2   d x

Vamos resolver as duas integrais:

∫ 0 x r 395 x - 0,5   d x =   395 x - 0,5 + 1 - 0,5 + 1 0 x r = 395 x 0,5 0,5 0 x r = 790 x r 0,5

∫ x r L 2330 x - 0,2   d x = 2330 x - 0,2 + 1 - 0,2 + 1 x r L = 2912,5 x 0,8 0,8 x r L = 2912,5 L 0,8 - x r 0,8

Vamos agora substituir os valores e calcular h - ( x r ) :

h - x r = 790 x r 0,5 - 2912,5 x r 0,8 + 2912 , 5 0,6 0,8 0,6 = 1316,7 x r 0,5 - 4854,17 x r 0,8 + 3225,8

Passo 3

Agora, pra fechar a questão, vamo pegar a função que a gente definiu e plotar um gráfico no Excel de 0 ≤ x r ≤ 0,6:

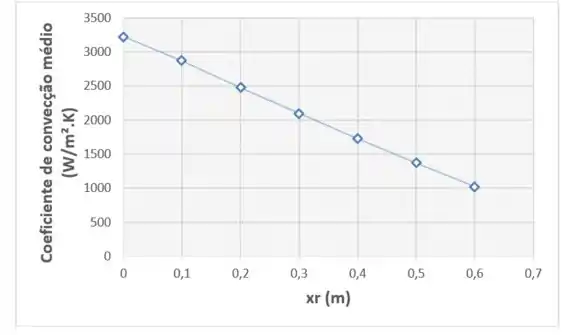
Analisando o gráfico, podemos ver que nesse intervalo determinado, o valor máximo de h - ocorre em x r = 0 e o valor mínimo em x r = 0,6 .

Sendo assim:

h - m á x = 3226 W m 2 . K

h - m i n = 1020,5 W m 2 . K

Pronto, matamos a questão juntos! :)

Resposta

Os valores máximo e mínimo do coeficiente de convecção médio são, respectivamente:

h - m á x = 3226 W m 2 . K

h - m i n = 1020,5 W m 2 . K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Demonstre a equação: p p ∞ = 1 + y A M A M B - 1
Procure adaptar os quadros 7.1 ,7.2 ,8.1 ,( 8.2 ) à convecção mássica natural
Para mistura binária diluída, demonstre, via análise de escala, que:a) ∂ ∂ x ρ u + ∂ ∂ y ρ v = ∂ u ∂ x + ∂ v ∂ y .b) u ∂ ρ A ∂ x + ∂ p A ∂ y - D A B ∂ 2 ρ A ∂ x 2 = u ∂ w A ∂ x + ∂ w A ∂ y - D A B ∂ 2
Demostre, para uma mistura gasosa não-ideal e diluída, que:a) p p ∞ = 1 + y A ϕ 1 + y A ϕ b) k = ϕ - θ 1 + y A θ 2
O uso de jatos de ar colidentes é proposto como um meio efetivo para resfriar circuitos integrados (chips) lógicos de alta potência em um computador. Contudo, antes que essa técnica possa ser implemen