A superfície superior de uma placa de alumínio anodizado com espessura é irradiada com , estando simultaneamente exposta a condições convectivas caracterizadas por . A parte de trás da placa encontra-se isolada termicamente. Para uma temperatura da placa de , assim como e, determine a radiosidade na superfície superior da placa, o fluxo radiante líquido na superfície superior, e a taxa na qual a temperatura da placa varia com o tempo.
Passo 1
Oii, turubom?! Vamos passar um Raio X nesse exercício para ver o que ele quer da gente? 😊 Nessa questão nós temos a espessura e temperatura de uma chapa de alumínio. Além da irradiação, condições de convecção, absorção e emissividade. Esquematicamente:
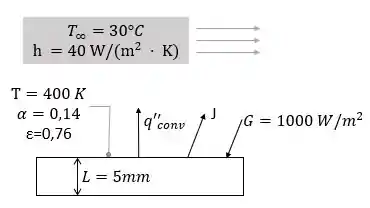
Com essas informações vamos encontrar a radiosidade, o fluxo de calor da radiação líquida na superfície da placa superior e a taxa de variação da temperatura da placa, beleza? Então vem comigo!
Passo 2
Para resolver essa questão vamos assumir que a temperatura da placa é uniforme e que a placa é opaca, ou seja,, beleza?
A nossa querida radiosidade vai ser igual à soma da radiação emitida e refletida:
Substituindo os valores ficamos com:
Passo 3
Primeira etapa já foi, agora precisamos encontrar o fluxo líquido de calor da radiação da placa. Que é igual à radiosidade menos a irradiação:
Passo 4
E por último, mas não menos importante (rufem os tambores)... A taxa de variação da temperatura da placa! Ela pode ser encontrada através de um balanço energético da placa, responsável pela perda de calor por radiação e convecção,
Substituindo os valores,
Agora sim fizemos tudo o que o enunciado nos pediu \o/