Um aquecedor elétrico de cartucho possui a forma de um cilindro, com comprimento e diâmetro externo . Em condições normais de operação, o aquecedor dissipa quando submerso em uma corrente de água a em que o coeficiente de transferência de calor por convecção é de . Desprezando a transferência de calor nas extremidades do aquecedor, determine a sua temperatura superficial . Se o escoamento da água for inadvertidamente eliminado e o aquecedor permanecer em operação, sua superfície passa a estar exposta ao ar, que também se encontra a , mas para o qual . Qual é a temperatura superficial correspondente? Quais são as consequências de tal evento?
Passo 1
A questão nos deu as dimensões do aquecedor elétrico de cartucho, sua potência e os coeficientes de convecção do ar e da água a uma temperatura específica. Para ficar mais claro, vamos desenhar isso então.
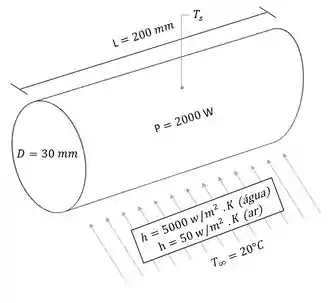
A partir disso, precisamos calcular a temperatura da superfície do aquecedor, , tanto na água quanto no ar. Então, vamos lá para as nossas considerações!
Passo 2
Para resolver esta questão vamos assumir que:
- Estamos na condição de estado estacionário;
- Todo a energia elétrica é transferida para o fluído de convecção;
- A transferência de calor nas extremidades é insignificante.
Essas considerações você não precisa necessariamente escrever na prova, depende muito do seu professor, se ele vai exigir isso de você ou não, beleza? Vamos continuar então...
Agora, podemos aplicar a Lei Newton para o resfriamento,
Ou seja,
Repara que é a área superficial do cilindro, por isso que . Isolando o ,
Como já temos uma fórmula para , podemos, finalmente, aplicar os valores para a água e o ar.
Passo 3
Para a água temos que,
Já para o ar,
Consequentemente, o ar é muito menos eficaz que a água como fluido de transferência de calor. Portanto, a temperatura do cartucho é muito mais alta no ar, tão alta que o cartucho derrete.
Resposta
Como consequência o cartucho derrete quando o fluido de convecção for o ar.