Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 82
Um tanque esférico com diâmetro externo de 1 m está localizado ao ar livre a 1 atm e 25°C e está sujeito a ventos de 35 km/h. Determine a força de arrasto exercida sobre ele pelo vento.
Passo 1
E aí, como você tá? Vem aqui comigo pra gente resolver esse problema juntos!
Nessa questão, a gente tem uma esfera de diâmetro sob um escoamento externo de ar com velocidade de (), a e C.
A questão requer que a gente calcule a força de arrasto exercida pelo vento na esfera, a partir da equação:
Sendo a área frontal da esfera a massa específica do ar, a velocidade do ar e o coeficiente de arrasto da esfera.
Para obter o coeficiente devemos antes calcular o número de Reynolds para o escoamento externo numa esfera a partir da equação:
Sendo a viscosidade cinemática do ar.
Antes da gente ir pro próximo passo a gente precisa buscar algumas propriedades do ar a na Tabela A-9 (página 779):
Agora sim, vem comigo pra gente resolver esse problema juntos!
Passo 2
Vamo começar então. A parte mais importante desse problema é encontrar o valor do coeficiente de arrasto.
Pra isso, a gente vai primeiro calcular o número de Reynolds para o problema:
Agora pra encontrar o valor do coeficiente de arrasto para esse escoamento, devemos ir na Figura 11-34 (página 511).
Vamos entrar com o valor do número de Reynolds que acabamos de descobrir no eixo das abscissas e obter a resposta de no eixo das ordenadas, como eu vou demonstrar pra você na figura abaixo:
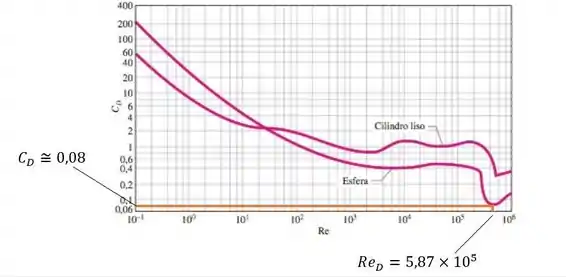
Como você pode ver na imagem a cima, a gente usou uma linha laranja partindo do valor de nas abcissas, que tocou a curva da esfera no diagrama, pra encontrar o valor de correspondente no eixo das ordenadas.
Pra finalizar a questão, vamos calcular a força de arrasto substituindo os valores que a gente encontrou na equação definida no Passo 1:
Pronto, matamos a questão juntos!
Resposta
A força de arrasto exercida sobre o tanque esférico pelo vento é .