Uma bola lisa de 8 cm de diâmetro tem uma velocidade de 36 km/h durante uma rebatida típica. Determine o aumento percentual no coeficiente de arrasto se for aplicada à bola uma rotação de 3500 rpm no ar a 1 atm e 25°C.

Vamo começar então calculando o para a situação em que não temos uma rotação aplicada.

Pra isso, primeiro a gente calcula o número de Reynolds com a equação aí embaixo:

Agora com esse resultado pro número de Reynolds a gente vai no diagrama da Figura 11-36 (página 512), que relaciona e para esferas de diferentes rugosidades.

Analisando a curva para uma esfera lisa, a gente chega a:

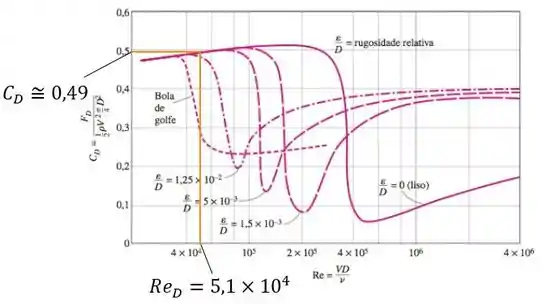
Olha essa linha laranja ali no gráfico. Quero que você repare que a gente puxou ela partindo da abscissa do valor de Reynolds de que calculamos, cruzou com a curva pra uma esfera lisa e encontrou o valor de na linha das ordenadas.

Esse é o procedimento que a gente tem que utilizar pra resolver esse tipo de questão.

Agora, a gente vai calcular o coeficiente de arrasto quando aplicada uma rotação de utilizando uma raquete.

Pra isso, primeiro a gente calcula a taxa de rotação adimensional com a equação aí embaixo:

Agora com esse resultado, a gente vai no diagrama da Figura 11-53 (página 520). Analisando a curva que relaciona e , a gente chega a:

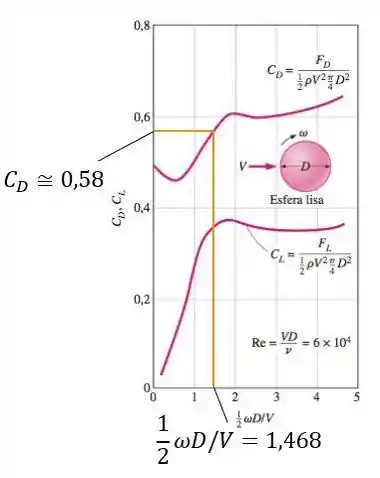
Vamo olhar de novo pra linha laranja ali no gráfico.

De novo, a gente parte da abscissa no valor de que calculamos, cruza com a curva pro coeficiente de arrasto e obtemos um valor de na linha das ordenadas.

Agora, pra finalizar a questão, a gente vai calcular o aumento percentual no coeficiente de arrasto pra quando a gente faz a rotação com a raquete:

Ou seja, a rotação causada com a raquete aumenta o coeficiente de arrasto aumenta .

Agora sim, terminamos de matar a questão juntos!