Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 23
No tanque da figura, determinar a força que deve ser aplicada para que ele permaneça parado. Qual é o diâmetro do bocal que deverá ser instalado na parede oposta ao bocal mostrado na figura, para que a força provocada por esse novo jato venha a substituir o efeito da força ? Esse novo bocal será instalado a 1 m de profundidade e admite-se que a sua perda de carga seja igual à do bocal da figura. Desprezar o atrito nas rodas. Dados: ; .
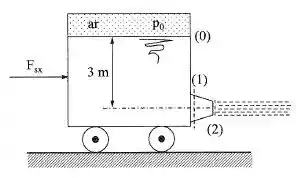
Passo 1
Vamos começar esse exercício aplicando o equilíbrio de cargas entre os pontos 0 e 2:
Substituindo os valores conhecidos:
Agora vamos aplicar a equação da força que o fluido exerce sobre um anteparo, nesse caso, para os pontos 1 e 2, então a equação se torna:
Vamos calcular a equação na direção :
Podemos escrever a vazão mássica como:
Substituindo essa relação na equação para a força, temos:
Como essa é a força que o fluido exerce no sistema, então, para obter basta trocar o sinal, então, temos:
Substituindo os valores conhecidos, temos:
Passo 2
Agora, com a nova configuração do sistema, vamos aplicar novamente o equilíbrio de cargas entre os pontos 0 e 2:
Substituindo os valores conhecidos:
Agora vamos aplicar a equação da força que o fluido exerce sobre um anteparo, nesse caso, para os pontos 1 e 2, então a equação se torna:
Vamos calcular a equação na direção :
Podemos escrever a vazão mássica como:
Substituindo essa relação na equação para a força, temos:
Como essa é a força que o fluido exerce no sistema, então, para obter basta trocar o sinal, então, temos:
Substituindo os valores conhecidos, temos: