Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 11
A asa de um avião tem 7,5 m de envergadura e 2,1 m de corda. Estimar a força de arrasto na asa utilizando os resultados para o escoamento sobre uma placa plana e admitindo a camada limite turbulenta desde o bordo de ataque, quando o avião voa a 360 km/h. Qual seria a redução de potência necessária se fosse feito o controle da camada limite de forma a assegurar escoamento laminar até o bordo de fuga? ;
Passo 1
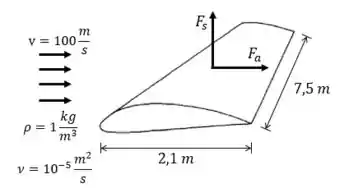
Dados da questão:
- Envergadura:
- Corda:
- Velocidade:
- Escoamento em regime turbulento
- Viscosidade do ar:
- Densidade do ar:
A questão pede:
- A força de arrasto:
- Quanto a mais de potência de arrasto é consumida comparado a um escoamento laminar
Passo 2
Primeiro, vamos calcular os coeficientes de arrasto. Vamos fazer a seguinte consideração: para o caso do escoamento sobre uma asa, o arrasto de superfície é muito grande e o arrasto de pressão é desprezível.
Para o escoamento turbulento temos:
Para um escoamento laminar temos:
Passo 3
Agora podemos calcular as forças de arrasto pela equação:
Observe que a questão diz: “utilizando os resultados para o escoamento sobre uma placa plana”. Isso quer dizer que temos que considerar tanto a área superior quanto a área inferior da asa (isto é, duas vezes a área da superfície):
Aplicando na equação do arrasto:
Chegamos na expressão:
Aplicando para o regime turbulento:
Aplicando para o regime laminar:
Passo 4
A potência é dada por:
Para calcular a diferença de potência em porcentagem, vamos considerar a potência gerada por cada regime:
A diferença percentual de potência será: