Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 12

Determinar a relação entre a velocidade constante de subida de uma bolha de ar de diâmetro 1mm dentro da água e a velocidade constante de descida de uma gota de água de mesmo diâmetro no ar. Dados: ρ = 1   k g / m 3 ; ρ H 2 O = 1000   k g / m 3 ; C a = 0,5

Passo 1

Dados da questão:

  • Diâmetro: d = 1   m m
  • Densidade do ar: ρ = 1   k g / m 3
  • Densidade da água: ρ H 2 O = 1000   k g / m 3
  • Coeficiente de arrasto: C a = 0,5

Note que em cada um dos casos vamos fazer algumas considerações. Devido à baixa densidade do ar, podemos desconsiderar o peso da bolha de ar, e podemos desconsiderar o empuxo que o ar gera numa gota.

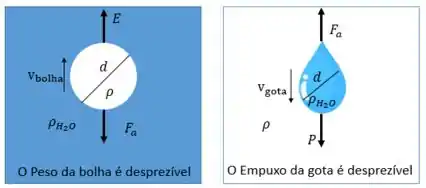
A questão pede: A razão entre as velocidades

Passo 2

Para a bolha nós temos:

E = F a

Substituindo as fórmulas do empuxo e do arrasto:

ρ H 2 O ⋅ g ⋅ V b o l h a = C a ⋅ ρ H 2 O ⋅ v b o l h a 2 ⋅ A 2

Substituindo a equações do volume e da área:

ρ H 2 O ⋅ g ⋅ 1 8 π D 3 = C a ⋅ ρ H 2 O ⋅ v b o l h a 2 ⋅ π D 2 4 2

Simplificando a equação:

v b o l h a 2 = g D C a

Aplicando os valores:

v b o l h a = 10 m s 2 ⋅ 10 - 3   m 0,5

v b o l h a = 0,02 m s

Passo 3

Para a gota de água:

P = F a

Substituindo as fórmulas do peso e do arrasto:

ρ H 2 O ⋅ g ⋅ V g o t a = C a ⋅ ρ ⋅ v g o t a 2 ⋅ A 2

Substituindo a equações do volume e da área:

ρ H 2 O ⋅ g ⋅ 1 8 π D 3 = C a ⋅ ρ ⋅ v g o t a 2 ⋅ π D 2 4 2

Simplificando a equação:

v g o t a 2 = ρ H 2 O ⋅ g ⋅ D C a ⋅ ρ

Aplicando os valores:

v g o t a = 1000 k g m 3 ⋅ 10 m s 2 ⋅ 10 - 3   m 0,5 ⋅ 1 k g m 3

v g o t a = 20 m s

Passo 4

Dividindo as velocidades:

v g o t a v b o l h a = 20 0,02

v g o t a v b o l h a = 31,62

Resposta

v g o t a v b o l h a = 31,62

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aleta vertical estabilizadora sobre um carro de recorde de velocidade tem comprimento L = 1,65m e altura H = 0,785m . O automóvel deve ser dirigido na pista de Bonneville Salt Flats, em Utah, onde
O deslocamento de um superpetroleiro é aproximadamente de 600 . 000 toneladas métricas. Esse navio tem comprimento L = 300m , través (largura) b = 80m e calado (profundidade) D = 25m . O cargueiro nav
Um submarino nuclear navega a 13,9m / s , inteiramente submerso. O casco é aproximadamente um cilindro circular de diâmetro D = 11,0m e comprimento L = 107m . Estime a porcentagem do comprimento do ca
O avião de transporte a jato de 600 lugares proposto pela Indústria Airbus tem uma fuselagem de 70m de comprimento e 7,5m de diâmetro. O avião deve operar 14 horas por dia, 6 dias por semana; sua velo
Na Seção 7.6, a resistência de onda e a resitência viscosa sobre um modelo e sobre um protótipo de navio foram discutidas. Para o protótipo, L = 130m e A = 1800m 2 . A partir dos dados das Figs. 7.2 e