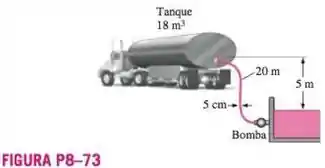
Um tanque ventilado deve ser enchido com óleo combustível com e de um reservatório subterrâneo, usando uma mangueira plástica de 20 m de comprimento e 5 cm de diâmetro, com uma entrada ligeiramente arredondada e duas curvas suaves de . A diferença de elevação entre o nível do óleo do reservatório e a parte superior do tanque onde a mangueira é descarregada é de 5 m. A capacidade do tanque é de 18 m³ e o tempo de preenchimento é de 30 min. Considerando que o fator de correçäo da energia cinética na descarga da mangueira seja 1,05 e supondo uma eficiência geral da bomba de 82%, determine a entrada necessária de potência na bomba.

Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:

Escolhemos o ponto 1 na superfície livre de óleo no reservatório e o ponto 2 na saída da mangueira.

Observamos que o fluido em ambos os pontos está aberto para a atmosfera (e, portanto, ) e a velocidade do fluido no ponto 1 é zero (). Tomamos a superfície livre do reservatório como o nível de referência (). Então a equação de energia para o volume de controle entre esses dois pontos simplifica a:

Onde a perda de carga é encontrada pela equação da perda de carga menor somado com a perda de carga maior, assim:

A vazão, o número de Reynolds, e o fator de atrito em cada tubo são expressos como:

E

Agora, o número de Reynolds é expresso:

E o fator de atrito é expresso como:

Resolvendo de forma iterativa (ferramenta Solve, do Excel), encontramos .

A perda de carga total é expressa como:

Assim:

E por fim, substituindo os valores na equação 2:

Portanto, a entrada necessária de potência na bomba pode ser determinada por:

Obs: O números de Reynolds está na ordem de , portanto a verificação se o regime é turbulento foi realizada.