Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 64
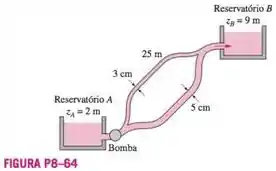
Água a deve ser bombeada de um reservatório para outro reservatório a uma elevação mais alta através de dois tubos de plástico com 25 m de comprimento conectados em paralelo. Os diâmetros dos dois tubos são 3 cm e 5 cm. A água deve ser bombeada por uma unidade de bomba-motor com eficiência de 68%, que consome 7kW de energia elétrica durante a operação. As perdas menores e a perda de carga dos tubos que conectam os tubos paralelos aos dois reservatórios são consideradas desprezíveis. Determine a vazão total entre os reservatórios e as vazões através de cada um dos tubos paralelos.
Passo 1
Oi pessoal, tudo bem?
Primeiramente, para o problema, assumimos que:
1. O fluxo é constante e incompressível.
2. Os efeitos de entrada são insignificantes e, portanto, o fluxo é totalmente desenvolvido.
3. As elevações dos reservatórios permanecem constantes.
4. As perdas menores e a perda de carga em tubulações que não sejam os tubos paralelos são considerados insignificantes, como informa o enunciado.
5. Definimos que os fluxos através ambos os tubos são turbulentos (a serem verificados).
6. Tubos de plástico são lisos e sua rugosidade é zero, ε = 0.
E se observarmos atentamente, vamos ver que este problema não pode ser resolvido diretamente, pois as velocidades (ou vazões) nos tubos não são conhecidas. Portanto, normalmente usaremos uma abordagem de tentativa e erro aqui.
Passo 2
Inicialmente, a potência fornecida pela bomba é informada por:
Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:
Do problema, temos:
Obs: propriedades da água à , Tabela A.3 do livro.
Enfim, escolhemos os pontos A e B nas superfícies livres dos dois reservatórios para a análise.
Observando que o fluido nos dois pontos está aberto para o atmosfera (e, portanto) e que as velocidades do fluido nos dois pontos são zero (), a equação da energia (Eq. 1) para um volume de controle entre esses dois pontos simplifica:
Passo 3
Designamos o tubo de 3 cm de diâmetro por 1 e o tubo de 5 cm de diâmetro por 2. A velocidade média, número de Reynolds, fator de atrito e a perda de carga em cada tubo são expressos como:
Agora, o número de Reynolds em cada tubo é expresso como:
E o fator de atrito em cada tubo é expresso como:
Por fim, a perda de carga em cada tubo é expressa como:
Então, podemos perceber que as correlações dependem das velocidades 1 e 2, para finalmente encontrarmos os valores das vazões em cada tanque.
Passo 4
Portanto, as equações formam um conjunto de equações simultâneas, nas quais podemos resolver iterativamente (por meio do excel, ou outra ferramenta computacional):
A solução utiliza a ferramenta Solve, que consiste em assumir valores iniciais para as velocidades 1 e 2, e o cálculo das demais variáveis ocorre, retornando a um novo valor das velocidades em 1 e 2.
Então, esse processo é feito até os valores das velocidades 1 e 2 supostas no início coincidirem com as do resultado final, ou com um erro bem pequeno.
Realizando esse processo na ferramenta descrita, encontramos que:
E
Obs: Os números de Reynolds respectivos estão na ordem de , portanto a verificação se o regime é turbulento foi realizada.
Resposta
Portanto: