Os tanques A e D são de grande dimensões e o tanque C é de pequenas dimensões, mas o nível (4) permanece constante. A bomba B, que tem , recebe 11 kW do motor elétrico e tem carga manométrica de 20 m. Determinar:
a) o tipo de máquina M e sua carga manométrica;
b) a vazão no trecho (4)-(5) (L/s);
c) a vazão que passa na bomba B (L/s);
d) a cota z (m).
Dados: .
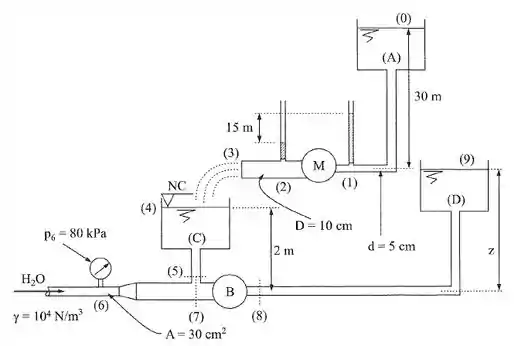
Passo 1
Vamos começar o exercício analisando a relação entre os pontos 1 e 2, sabemos que a vazão nesses pontos devem ser iguais, então:
Substituindo os valores conhecidos:
Agora, vamos aplicar o equilíbrio de cargas entre os pontos 1 e 2:
Agora vamos isolar a carga da máquina:
Agora, já vimos que então o termo anterior de velocidade é negativo, e como podemos ver pelos manômetros da figura nos pontos 1 e 2, sabemos que , então o termo será negativo, o que quer dizer que o fluido fornece energia para a máquina, então, nesse caso, temos uma turbina.
Agora podemos escrever a equação de equilíbrio de carga entre os pontos 0 e 3:
Agora, substituindo os valores conhecidos:
Essa será nossa equação 1. Agora, voltando a equação obtida do equilíbrio entre os pontos 1 e 2:
Podemos substituir a relação obtida para e também a diferença de pressão aferida pelo manômetro da figura (lembrando do sinal negativo já que a máquina é uma turbina):
Como 2 e 3 possuem a mesma vazão e mesmo diâmetro, então , então, substituindo a equação 1 a essa equação, temos:
Então, retornando a equação da carga da máquina, temos:
Passo 2
Agora para a letra b) através do desenho conseguimos ver que a vazão entre 4 e 5 é a mesma que vem do tanque A, que pode ser calvulada através da velocidade encontrada no passo 1 e a área nesse ponto, então, temos:
Passo 3
Agora, na letra c) vamos calcular a vazão da bomba através da fórmula de sua potência, dada por:
Passo 4
Agora para a resolver a letra d), vamos começar encontrando a vazão no ponto 6, pelo desenho sabemos que a vazão da bomba é a vazão em 6 mais a vazão que vem do tanque C, ou seja:
Com isso podemos encontrar a velocidade em 6 através da fórmula da vazão:
Agora podemos calcular a carga no ponto 6, que será:
Agora, aplicando o princípio da conservação de energia para o sistema, temos:
Podemos simplificar o termo que aparece multiplicando todos os termos, então substituindo os valores conhecidos:
Passo 5
E, agora, usando a fórmula da carga para o ponto 9, temos: