Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 10

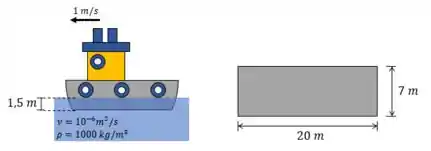
Uma barcaça de casco chato de 20 m de comprimento e 7 m de largura está imersa em profundidade de 1,5 m e deve ser empurrada com uma velocidade de 3,6 km/h. Estimar a potência necessária para efetuar o serviço se ν = 10 - 6   m 2 / s   e ρ = 1000   k g / m 3 .

Passo 1

Dados da questão:

  • Dimensões do casco: 20 × 7   m
  • Imersão do casco: 1,5   m
  • Velocidade v = 3,6   k m / h = 1   m / s
  • Viscosidade do fluido: ν = 10 - 6   m 2 / s
  • Densidade do fluido: ρ = 1000   k g / m 3 .

Para resolver esta questão, a área de superfície do casco é diferente da área frontal do casco. Por isso, vamos calcular as forças de arrasto de forma e de superfície separadamente. Com a soma deles termos o arrasto total. Depois basta multiplicar pela velocidade para ter a potência consumida.

Passo 2

Para calcular a área frontal do casco vamos considerar a região submersa:

A f = 7 ⋅ 1,5 = 10,5   m 2

A área de referência de superfície do casco é a área superior mais as duas áreas laterais (essa área também é conhecida como “área molhada”):

A s = 7 ⋅ 20 + 2 ⋅ 1,5 ⋅ 20 = 200   m 2

Passo 3

De acordo com o livro texto (página 236) podemos considerar o coeficiente de arrasto de forma como:

C a p = 1,2

Podemos calcular o arrasto de forma usando a equação do arrasto:

F a p = C a p ⋅ ρ ⋅ v 2 2 A f

Aplicando os valores:

F a p = 1,2 ⋅ 1000 ⋅ 1 2 2 10,5

F a p = 6300   N

Passo 4

Para calcular o coeficiente de arrasto de superfície vamos considerar o escoamento turbulento, pois essa é a situação que consumirá maior potência de arrasto.

C a s = 0,074 R e 5

C a s = 0,074 ⋅ ν v ⋅ L 5

C a s = 0,074 ⋅ 10 - 6   m 2 / s 1   m / s ⋅ 20   m 5

C a s = 2,56 ⋅ 10 - 3

Passo 5

Vamos aplicar agora na equação no arrasto de superfície:

F a s = C a s ⋅ ρ ⋅ v 2 2 A s

F a s = 2,56 ⋅ 10 - 3 ⋅ 1000 ⋅ 1 2 2 ⋅ 200

F a s = 256   N

Passo 6

A força de arrasto total é:

F a = F a s + F a p

F a = 6300 + 256

F a = 6556   N

Passo 7

Logo, a potência consumida pelo arrasto é:

N = F ⋅ v

N = 6556 ⋅ 1

N = 6556   W

N = 6,56   k W

Resposta

N = 6,56   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No teste de um veículo, num túnel aerodinâmico, foi levantada a curva de potência gasta para vencer a força de arrasto do ar em função de sua velocidade. Sendo a vista frontal do veículo indicada na f
A asa de um avião tem 7,5 m de envergadura e 2,1 m de corda. Estimar a força de arrasto na asa utilizando os resultados para o escoamento sobre uma placa plana e admitindo a camada limite turbulenta d
Num viscosímetro de esfera, uma esfera de aço de massa específica ρ = 7.800k g / m 3 e diâmetro 1m m afunda num líquido de massa específica ρ = 800k g / m 3 , com uma velocidade limite de 2c m / s . C
Determinar a relação entre a velocidade constante de subida de uma bolha de ar de diâmetro 1mm dentro da água e a velocidade constante de descida de uma gota de água de mesmo diâmetro no ar. Dados: ρ
Uma placa de 0,9 m x 1,2 m move-se com 13,2 m/s em ar parado, com uma inclinação de 12º com a horizontal. Sendo C a = 0,17 ; C s = 0,72 ; ρ = 1,2k g / m 3 ; A=área de referência = área da placa, deter