Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 64

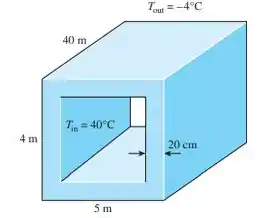
Um forno de 5 m de largura, 4 m de altura e 40 m de comprimento usado para curar tubos de concreto é feito de paredes e teto de concreto k =   0,9   W   m   ·   K de 20 cm de espessura. O forno é mantido a 40°C por injeção de vapor quente. As duas extremidades do forno, de 4   m × 5   m de dimensão, são feitas de chapa de metal 3 mm de espessura coberta com isopor k =   0 , 033   W   m   ·   K   de 2 cm de espessura. Os coeficientes de transferência de calor por convecção das superfícies interna e externa do forno são de 3000 W m 2   ·   K   e 25 W m 2   ·   K , respectivamente. Desconsiderando qualquer perda de calor no piso, determine a taxa de perda de calor do forno quando o ar ambiente estiver a -4°C.

Passo 1

Beleza galera, vamos lá!!

O que está acontecendo aqui é o seguinte, o forno perde calor pelo teto e pelas laterais. Mas não só por ai, ele também perde pelas extremidades.

Então teremos duas formas de perda de calor, certinho?

Para o topo e as laterais teremos:

Vamos calcular as resistências?

R d e n t r o = 1 h d e n t r o × A d e n t r o

R c o n c r e t o = L k c o n c r e t o × A c o n c r e t o

R f o r a = 1 h f o r a × A f o r a

Agora a grande questão aqui é qual será a área, não é verdade?

Vamos começar pela área de fora, e vamos considerar que os lados e o topo formam um grande retângulo, de altura igual a 40 m e para a altura nós somaremos os lados, 4m + 4m + 5m:

A f o r a = 40   m × 13 m = 520   m 2

Para área de dentro nós teremos a altura de 13 m menos a espessura de 20 cm dos três lados:

A d e n t r o = 40   m × ( 13 - 3 × 0,2 ) m = 496   m 2

E para a área do concreto nós faremos uma média entre as duas:

A c o n c r e t o = 520   m 2 + 496   m 2 2 = 508   m 2

Agora vamos lançar nossos dados:

R d e n t r o = 1 3000 W m 2   ·   K × 496   m 2 = 6,7 × 10 - 7 K W

R c o n c r e t o = 0,2   m 0,9   W   m   ·   K × 508   m 2 = 4,37 × 10 - 4 K W

R f o r a = 1 25 W m 2   ·   K × 520   m 2 = 7,69 × 10 - 5 K W

Como estão todas em série:

R l a d o s   e   t e t o = R d e n t r o + R c o n c r e t o + R f o r a

R l a d o s   e   t e t o = 5,15 × 10 - 4 K W

Para a taxa de calor nós já estamos carecas de saber como calcular, né verdade?

Q l a d o s   e   t e t o ˙ = ∆ T R l a d o s   e   t e t o

Substituindo:

Q l a d o s   e   t e t o ˙ = 40 ° C - ( - 4 ° C ) 5,15 × 10 - 4 K W

Como a variação em graus Celsius é a mesma que a variação em kelvin:

Q l a d o s   e   t e t o ˙ = 85,4 × 10 3   W

Beleza galeraaa, agora só precisamos achar a perda de calor pelas extremidades!

Passo 2

Agora nas extremidades nós temos o isopor, certo?

E se desenharmos as novas resistências teremos:

Á sabemos como calcular as resistências, só precisamos das novas áreas.

A área de fora forma um retângulo com 4 m de altura e 5 m de comprimento:

A f o r a = 4   m × 5 m = 20   m 2

Para área de dentro nós teremos a altura de 4 m menos a espessura de 20 cm dos lados superior e inferior, a mesma coisa nas laterais:

A d e n t r o = ( 4   - 0,4 ) m × ( 5 - 0,4 ) m = 16,56   m 2

E para a área do isopor nós faremos uma média entre as duas:

A i s o p o r = 20   m 2 + 16,56   m 2 2 = 1 8,28   m 2

Agora vamos lançar nossos dados:

R d e n t r o = 1 3000 W m 2   ·   K × 16,56   m 2 = 2,01 × 10 - 5 K W

R i s o p o r = 0 , 0 2   m 0,033   W   m   ·   K × 18,28   m 2 = 0,033 K W

R f o r a = 1 25 W m 2   ·   K × 20   m 2 = 0,002 K W

Como estão todas em série:

R e x t r e m i d a d e = R d e n t r o + R i s o p o r + R f o r a

R e x t r e m i d a d e = 0,0352 K W

Jogando no calor:

Q e x t r e m i d a d e ˙ = 40 ° C - ( - 4 ° C ) 0,0352 K W = 1,25 × 10 3   W

Passo 3

Então a troca de transferência total será dada pela soma dessas duas taxas.

Mas não se esqueça, temos duas extremidades:

Q T ˙ = Q l a d o s   e   t e t o ˙ + 2 Q e x t r e m i d a d e ˙

Q T ˙ = 88 × 10 3   W

Ou melhor:

Q T ˙ = 88   k W

Gostaram?

Resposta

Q T ˙ = 88   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No projeto de edifícios, a necessidade de conservação de energia exige que a área da superfície externa, As, seja minimizada. Essa exigência implica que, para uma dada área de piso desejada, devem exi
Trabalhe o Problema 3.15 supondo que as superfícies paralelas à direção x sejam adiabáticas.
29 - Água quente é transportada de uma estação de cogeração de potência para usuários comerciais e industriais através de tubos de aço com diâmetro D = 150m m . Cada tubo encontra-se no centro de um b
25 - Um pequeno dispositivo é usado para medir a temperatura superficial de um objeto. Uma junção de termopar, com diâmetroD=120μ m , está posicionada a uma distância z=100μ m da superfície de interes
22 - Uma janela de vidro duplo é constituída por duas folhas de vidro separadas por um espaço, com L = 0,2m m de espessura. Há vácuo neste espaço, o que elimina a condução e a convecção através dele.