Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 30
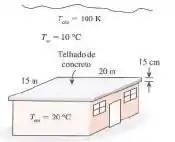
O telhado de uma casa consiste de laje de concreto de 15 cm de espessura, 15 m de largura, 20 m de comprimento. Os coeficientes de transferência de calor por convecção nas superfícies interna e externa do telhado são 5 e , respectivamente. Em uma noite clara de inverno, o ar ambiente está a 10 °C, enquanto a temperatura do céu noturno é 100 K. A casa e as superfícies internas das paredes são mantidas a uma temperatura constante de 20 °C. A emissividade de ambas as superfícies do telhado de concreto é 0,9. Considerando a transferência de calor por radiação e convecção, determine a taxa de transferência de calor através do telhado e a temperatura da superfície interna do telhado.
Se a casa é aquecida por forno queimando gás natural com eficiência de 80% e o preço do gás natural é US$ 1,20/therm (1 therm = 105500 kJ de energia), determine o dinheiro perdido através do telhado naquela noite durante o período de 14 horas.
Passo 1
Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!
Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e propriedades térmicas constantes.
Vejamos só. O calor flui de dentro da casa para fora, devido ao gradiente de temperatura. Como estamos trabalhando em regime permanente, a taxa que flui do ambiente interno é igual a taxa que flui pelo telhado que é igual a taxa que flui para o ambiente interno. Isto é:
À medida que começarmos a desenvolver as equações, ficará claro a necessidade de abordarmos o problema desta forma.
Passo 2
Agora, vamos desenvolver cada uma das equações para a taxa de transferência de calor. Portanto,
Não se esqueçam que a temperatura no termo de radiação deve estar em Kelvin! Continuando, temos:
Por fim,
E agora, conseguem perceber a sacada? Temos 3 equações e 3 incógnitas! Portanto, temos um sistema de equação!
O problema deste sistema é que ele não é linear. Portanto, precisamos da ajuda de softwares para resolver e assim obter os seguintes valores aproximados:
Passo 3
Para finalizarmos a questão, vamos calcular o custo perdido após a passagem da noite para mantermos a temperatura constante no ambiente interno.
Para isto, vamos começar calculando a energia necessária. Portanto,
Portanto, o custo é:
Resposta
A taxa de transferência de calor é:
A temperatura de saída é:
O custo para manter a temperatura interna foi de US$26,80.
A resistência térmica da parede é:
- Em unidades inglesas, a resistência térmica da parede é: