Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 7.Problemas - Ex. 16

O teto do baú de um caminhão refrigerado é construído com um material composto, sendo constituído por uma camada de isolante de espuma de uretano ( t 2 = 50   m m ,   k i = 0,026   W / ( m · K ) ) posicionada entre painéis de liga de alumínio ( t 1 = 5   m m ,   k p = 180   W / ( m · K ) ) . O comprimento e a largura do teto são L   =   1 2   m e W = 3,5   m , respectivamente, e a temperatura da superfície interna é T s , i = – 10 ° C . Sejam condições nas quais o caminhão se desloca a uma velocidade V = 1 10   k m / h , a temperatura do ar é T ∞ = 3 0 ° C e a irradiação solar é G s = 90 0   W / m 2 . Escoamento turbulento pode ser suposto ao longo de todo o teto.

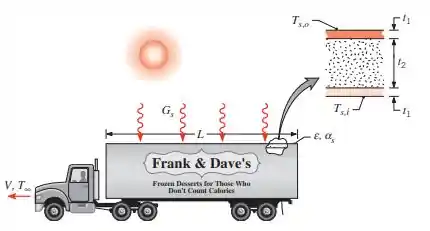
(a) Para valores equivalentes da absortividade solar e da emissividade da superfície externa ( α s = ε = 0 , 6 ) , determine a temperatura média da superfície externa T s , o . Qual é a carga térmica correspondente imposta ao sistema de refrigeração?

(b) Um acabamento especial ( α s = 0 , 2 ,   ε = 0,8 ) pode ser aplicado na superfície externa. Que efeito teria tal aplicação na temperatura superficial e na carga térmica?

Passo 1

Vem comigo resolver esse problema!

Se ajeita aí e vamos começar!

Começamos o nosso problema obtendo os dados para o ar na Tabela A.4 a 300   K e 1   a t m :

v = 15,89 × 10 - 6   m 2 / s

k = 0,0263   W / m ⋅ K

P r = 0,707

Bora começar os cálculos!

Passo 2

Letra a)

Aplicando um balanço de energia para a superfície externa do nosso sistema:

α S G S + q c o n v ' ' - E = q c o n d ' ' = T s , o - T s , i R t o t ' '

α S G S + h - T ∞ - T s , o - ε σ T s , o 4 = T s , o - T s , i 2 R p ' ' + R i ' '

Onde:

R p ' ' = t 1 k p = 0,005 180 = 2,78 × 10 - 5   m 2 ⋅ K / W  

R i ' ' = t 2 k i = 0,05 0,026 = 1,923   m 2 ⋅ K / W

Calculando R e L :

R e L = u ∞ L v = 30,5 ⋅ 10 15,89 × 10 - 6 = 1 , 92 × 10 7

Calculando h - :

h - = k L 0,037 R e L 4 5 P r 1 3 = 0,0263 12 ⋅ 0,037 ⋅ 1,92 × 10 7 4 5 ⋅ 0,707 1 3

h - = 48,5   W / m 2 ⋅ K

Passo 3

Substituindo os dados na equação para calcularmos a temperatura média da superfície externa:

0,6 ⋅ 900 + 48,5 ⋅ 305 - T s , o - 0,6 ⋅ 5,67 × 10 - 8 ⋅ T s , o 4 = T s , o - 263 2 ⋅ 2,78 × 10 - 5 + 1,923

T s , o = 309   K = 36 ° C

Calculando a carga térmica correspondente imposta ao sistema de refrigeração:

q = W L q f i n a l ' '

q = 3,5 ⋅ 12 ⋅ 36 + 10 1,923

q = 1004,7   W

Passo 4

Letra b)

Substituindo os dados na equação para calcularmos a temperatura média da superfície externa:

0 , 2 ⋅ 900 + 48,5 ⋅ 305 - T s , o - 0 , 8 ⋅ 5,67 × 10 - 8 ⋅ T s , o 4 = T s , o - 263 2 ⋅ 2,78 × 10 - 5 + 1,923

T s , o = 300,6   K = 27,6 ° C

Calculando a carga térmica correspondente imposta ao sistema de refrigeração:

q = W L q f i n a l ' '

q = 3,5 ⋅ 12 ⋅ 27,6 + 10 1,923

q = 821,2   W

Te espero na próxima questão!

Resposta

a )   T s , o = 309   K = 36 ° C

q = 956,6   W

b )   T s , o = 299,8   K = 26,8 ° C

q = 821,2   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é variável de similaridade e para que é utilizada? Para que tipos de funções pode-se esperar que exista solução por similaridade para o conjunto de equações diferenciais parciais?
Para escoamento bidimensional constante sobre uma placa plana isotérmica a uma direção x , expresse as condições de contorno para os componentes de velocidade u e v , e a temperatura T na superfície d
Para escoamento bidimensional constante, o que são aproximações da camada limite?
Expresse a equação da continuidade para escoamento bidimensional com propriedades constantes e explique o que cada termo representa.
Considere um escoamento laminar permanente bidimensional sobre placa isotérmica. A tensão de cisalhamento na parede aumenta, diminui ou permanece constante com a distância do bordo de ataque?