Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 16

If the absolute pressure at the interface between water and

mercury in Fig. P2.16 is 93 kPa, what, in lbf/ft2, is (a) the

pressure at the surface and (b) the pressure at the bottom of

the container?

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Água e mercúrio estão em um container como:

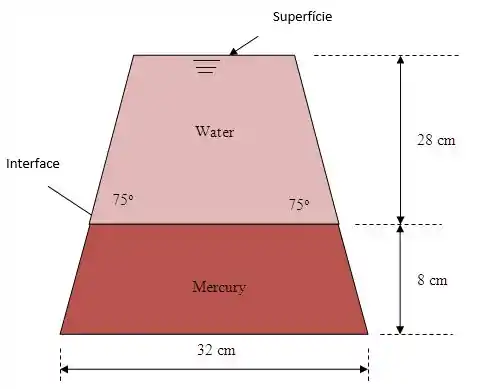
Passo 2

a) A pressão na interface é P i n t e r f a c e = 93000   P a

Calculando o peso da densidade da água

γ á g u a = ρ á g u a g = 998 ⋅ 9,81

→ γ á g u a = 9790   N / m 3

Calculando o peso da densidade do mercúrio

γ m e r c ú r i o = ρ m e r c ú r i o g = 16550 ⋅ 9,81

→ γ m e r c ú r i o = 132925,5   N / m 3

Passo 3

Calculando a pressão na superfície

P s u p e r f í c i e = P i n t e r f a c e - 0,28 γ á g u a = 93000 - 0,28 ⋅ 9790

→ P s u p e r f í c i e = 90258,8   P a

Convertendo as unidades de pressão pro sistema FPS

P s u p e r f í c i e = 90258,8   P a ⋅ l b f / f t 2 47,88   P a

∴ P s u p e r f í c i e = 1885,1   l b f / f t 2

Passo 4

b) A pressão na base do container é dada por

P b a s e = P i n t e r f a c e + 0,08 γ m e r c ú r i o

Substituindo calores

P b a s e = 93000 + 0,08 ⋅ 132925,5

→ P b a s e = 103634,04   P a

Convertendo para o sistema FPS

P b a s e = 103634,04   P a ⋅ l b f / f t 2 47,88   P a

∴ P b a s e = 2164,45   l b f / f t 2

Resposta

a) P s u p e r f í c i e = 1885,1   l b f / f t 2

b) P b a s e = 2164,45   l b f / f t 2

Exercícios de Livros Relacionados

Considere um homem de 1,80 m de altura em pé na água e completamente submerso em uma piscina. Determine a diferença entre as pressões que agem sobre a cabeça e os dedos desse homem em kPa.
Repita o problema 3-33 para uma pressão manométrica de 45 kPa.
A parte superior de um tanque de água está divida em dois compartimentos como mostrado na figura abaixo. Agora um fluido com uma densidade desconhecida é despejado de um lado e o nível da água sobe at
A pressão manométrica do ar no tanque mostrado é medida como 65 kPa. Determine a altura diferencial h da coluna de mercúrio.
A carga de 500 kg do macaco hidráulico mostrado na figura abaixo deve ser elevada despejando-se óleo ( ρ = 780k g / m ³ ³) dentro de um tubo fino. Determine quão alto h deve ser para começar a levanta