Nossos alunos efetuam um experimento de laboratório para determinar a transferência de massa em uma toalha de papel embebida em água, na qual há convecção forçada e irradiação de lâmpadas radiantes. Para os valores de T∞ e Tbu fornecidos na figura, determinou-se a temperatura da toalha igual a Ts = 310 K. Além disso, correlações para placas planas forneceram coeficientes convectivos médios de transferência de calor e de transferência de massa de = 28,7 W/(m2 · K) e m = 0,027 m/s, respectivamente. A toalha apresenta dimensões de 92,5 mm × 92,5 mm e é difusa e cinza, com uma emissividade de 0,96.

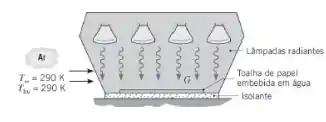
Com base nos resultados anteriores, determine as concentrações de vapor de água, ρA,s e ρA,∞, a taxa de evaporação, nA (kg/s), e a taxa de transferência de calor por radiação líquida para a toalha, qrad(W). (b) Usando os resultados da parte (a) e admitindo que a irradiação G é uniforme sobre a toalha, determine o poder emissivo E, a irradiação G e a radiosidade J.

Primeiro vamos começar com a letra a, assumindo que a corrente livre contém vapor de água em sua condição de saturação. Vamos visitar novamente a tabela A.6, sendo , teremos:

Beleza! Agora fazendo o balanço de energia teremos:

Precisamos achar a taxa de transferência por convecção, vamos lá:

Agora sim! Voltando na nossa equação original vamos ter:

Prontinho! Partiu letra b!

Agora na letra b, precisamos calcular três coisas diferentes! Vamos começar pelo poder emissivo, ok?

Podemos encontrar ele assim:

Show! Agora vamos achar a irradiação , pra isso podemos usar a relação dela com a taxa de radiação, assim olha só:

E pra finalizar, vamos achar radiosidade, sendo e :

Uhull! Arrasamos!