Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 101

Como um trabalho de laboratório de fluidos, foi solicitada a construção de um medidor para medir de forma aproximada, a vazão de água em um tubo de 45   m m de diâmetro. Você decide instalar um trecho de um tubo de 22,5   m m de diâmetro e um manômetro de tubo em U para medir a queda de pressão na contração súbita. Deduza uma expressão para a constante teórica de calibração k em Q = k ∆ h no qual Q é a vazão volumétrica em L / m i n e h é a deflexão no manômetro em m m . Trace a curva teórica de calibração para uma faixa de vazão de 10 a 50   L / m i n . Qual seria a sua expectativa de uso deste dispositivo como um real medidor de vazão?

Passo 1

A perda de carga é dada por:

p 1 ρ + V 1 2 2 + g z 1 - p 2 ρ + V 2 2 2 + g z 2 = h t

h t = K V 2 2 2 g

Sendo:

z 1 = z 2

Temos:

p 1 ρ + V 1 2 2 - p 2 ρ + V 2 2 2 = K V 2 2 2 g

p 1 - p 2 ρ = V 2 2 2 K + 1 - V 1 2 2

Passo 2

Aplicando a continuidade:

A 1 V 1 = A 2 V 2

V 2 = V 1 D 1 D 2 2

Substituindo na equação do Passo 1:

p 1 - p 2 ρ = V 1 2 2 D 1 D 2 4 K + 1 - V 1 2 2

∆ p = ρ V 1 2 2 D 1 D 2 4 1 + K - 1

Sendo:

V 1 = Q A 1

V 1 = Q π 4 D 1 2 = 4 Q π D 1 2  

Substituindo V 1 e fazendo a queda de pressão como:

∆ p = ρ g ∆ h

Temos:

ρ g ∆ h = ρ 2 4 Q π D 1 2 2 D 1 D 2 4 1 + K - 1

g ∆ h = 8 Q 2 π 2 D 1 4 D 1 D 2 4 1 + K - 1

Passo 3

Encontrando a vazão teórica:

Q = k ∆ h

Substituindo na equação do Passo 2:

g ∆ h = 8 k 2 ∆ h π 2 D 1 4 D 1 D 2 4 1 + K - 1

k = g π 2 D 1 4 8 D 1 D 2 4 1 + K - 1

Calculando a razão de área:

A R = D 2 D 1 2

Sendo:

D 1 = 45   m m ;

D 2 = 22,5   m m .

Temos:

A R = 22,5 45 2 = 0,25

Pelo gráfico “Coeficientes de perda para fluxo através de mudanças repentinas de área”, temos:

K = 0,4

Substituindo na equação principal:

k = 9,8 ⋅ π 2 ⋅ 45 x 10 - 3 4 8 1 0,25 2 1 + 0,4 - 1

k = 1,52 x 10 - 3   ( m 3 / s ) / m 1 2

k = 2,883   ( L / m i n ) / m m 1 2

Assim, a vazão em L / m i n é dada por:

Q ˙ = k ∆ h = 2,883 ∆ h

Passo 4

Traçando a curva teórica de calibração para uma faixa de vazão de 10 a 50   L / m i n :

Plotando o gráfico:

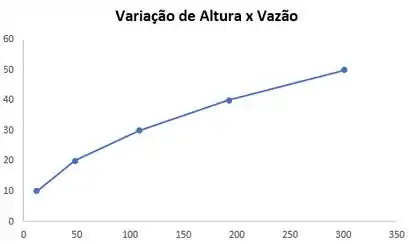
O dispositivo se mostra eficiente mesmo sendo uma curva não-linear.

Resposta

Q ˙ = 2,883 ∆ h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar a 20°C e aproximadamente 1 atm escoa a 42,5 m³/min por um duto liso de seção quadrada de 30 cm de lado. A queda de pressão esperada por metro de comprimento de tubo é1 Pa2 Pa3 Pa4 Pa5 Pa
Para o escoamento de óleo [ μ = 0,1k g / ( m . s ) , d = 0,9 ] a 14 m³/h por um tubo liso, reto e longo, de 5 cm de diâmetro, a queda de pressão por metro é aproximadamente2200 Pa2500 Pa10000 Pa160 Pa
Água a 20°C escoa por um tubo a 1,14 m3/min com uma perda de carga por atrito de 13,7 m. Qual é a potência necessária para manter esse escoamento?(a) 0,16 kW, (b) 1,88 kW, (c) 2,54 kW, (d) 3,41 kW, (e
Água a 20°C escoa a 3 m3/h por uma placa de orifício de 3 cm de diâmetro em um tubo de 6 cm de diâmetro. Calcule a queda de pressão esperada no orifício.(a) 440 Pa, (b) 680 Pa, (c) 875 Pa, (d) 1.750 P
Qual é a queda de pressão associada à água a 27° C fluindo com uma velocidade média de 0,1m / s através de um tubo de ferro fundido de 800m de comprimento de 0,30m no interiordiâmetro?