Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 8.Problemas - Ex. 3
Qual é a queda de pressão associada à água a fluindo com uma velocidade média de através de um tubo de ferro fundido de de comprimento de no interior
diâmetro?
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Então, antes de calcularmos a queda de pressão associada ao escoamento da água, precisamos saber qual tipo de escoamento nós temos.
Podemos classificar o escoamento como sendo laminar ou turbulento, e o que determina isso é o nosso amigo de sempre o número de Reynolds, quando ele é nosso escoamento é turbulento, se for será laminar. Para determinar o número de Reynolds :
Onde é a massa específica, é a velocidade do fluxo, é o diâmetro e é a viscosidade do fluído.
A partir da Tabela A.6, podemos encontrar os valores de viscosidade e a partir do volume específico podemos calcular a massa específica.
Antes de substituirmos na fórmula do , precisamos converter a viscosidade:
Agora aplicando os dados na fórmula, temos:
Lembra do que conversamos acima, sobre quando um escoamento é linear ou turbulento?
Então, o nosso Reynolds deu maior do que 2300, isso significa que o escoamento turbulento.
Passo 2
Como tempos um escoamento turbulento, iremos calcular a queda de pressão com a equação abaixo:
Para determinar a queda de pressão, primeiro precisamos determinar o fator de atrito, e para isso iremos usar a imagem abaixo:
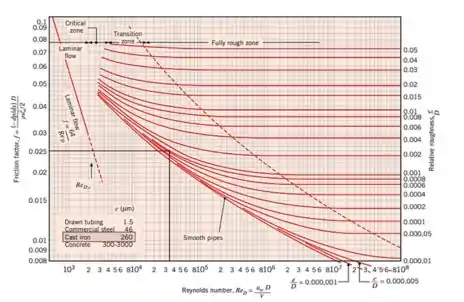
Para determinar o fator de atrito, primeiro vamos calcular a rugosidade relativa , a imagem nos diz que o ferro:
Olhando a imagem podemos inferir que:
Agora substituindo na equação para queda de pressão, temos:
Podemos deixar nossa pressão de um jeito mais elegante (utilizando o sistema internacional de medida):
Temos:
Foi divertido!!!!
Bora matar mais uma!