Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 78
Considere duas longas placas verticais mantidas a temperaturas uniformes . O espaço formado entre elas é aberto nas suas extremidades e as placas estão separadas pela distância .
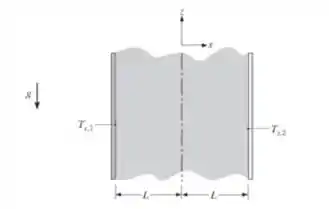
Esboce a distribuição de velocidades no espaço entre as placas.
Escreva formas apropriadas para as equações da continuidade, do momento e da energia para o escoamento laminar entre as placas.
Determine a distribuição de temperaturas e expresse seu resultado em termos da temperatura média,
(d) Estime o gradiente de pressão na direção vertical, admitindo que a massa específica seja uma constante correspondente a . Usando a aproximação de , obtenha a forma resultante da equação do momento.
(e) Determine a distribuição de velocidades.
Passo 1
Vamos lá, temos aqui um problema de canais verticais entre placas paralelas, onde as temperaturas entre as duas placas, são temperaturas prescritas de , o que é um dado muito importante.
E a placa é separada por uma distância de .
Passo 2
Iniciando a resolução pela questão , precisamos esboçar a distribuição de velocidades no espaço entre as placas.
Para realizarmos esse esboço, precisamos definir umas condições e a partir disso relembrar algumas definições...
Logo, assumindo propriedades constantes, ao longo de toda a física do problema, temos que para as condições prescritas, deve haver fluxos ascendentes e descendentes conduzidos por flutuabilidade ao longo das superfícies correspondentes a e .
Sabendo que , isso fará com que o fluido do lado com maior temperatura se expanda, fazendo com que sua densidade diminuía fazendo com que o fluido suba.
O lado com menor temperatura, fará com que o fluido fique mais denso, provocando sua queda.
Portanto, na simetria do plano, teremos a seguinte representação:
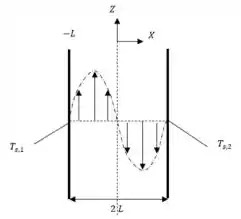
Passo 3
Partindo para questão , onde temos que determinar formas apropriadas para a equação da continuidade para o problema.
Precisamos lembrar antes que a equação genérica da continuidade é:
Essa equação é conhecida também como equação da conservação da massa e cada termo representa a velocidade em sua componente. Para fluidos em escoamento permanente e bidimensional, temos que para nosso problema:
Para placas longas , logo...
Como ambas as temperaturas são independentes de , a distribuição de temperatura totalmente desenvolvida também será:
Portanto, não há transferência líquida de momento ou energia por advecção (transmissão do calor pelo deslocamento de massa atmosférica no sentido horizontal), e as equações correspondentes são:
Passo 4
A questão , precisamos determinar a distribuição de temperaturas e expressar em termos de temperatura média.
Da equação anterior temos:
Realizando a integração dupla...
Note que iremos precisar aplicar as condições de contorno, o que corresponde ao espaçamento entre as placas partindo da simetria do plano, ou seja...
Determinado os coeficientes...
Note que , pois:
Portanto, aplicando os coeficientes na equação:
Passo 5
A questão , pede para estimarmos o gradiente de pressão na direção vertical, admitindo que a massa específica seja uma constante correspondente a.
Do exercício, ele nos pede pra usar a aproximação de Boussinesq, para obter a forma resultante da equação do momento.
Temos que o equilíbrio entre as forças de pressão gravitacional e líquida podem ser expressas como sendo:
Para obtermos a equação do momento, basta integramos a expressão acima, a qual ficará:
Realizando a aproximação de Boussinesq, que é:
Portanto...
Passo 6
Por fim, temos a questão , para determinarmos a distribuição de velocidades...
Portanto integrando a equação anterior duas vezes:
Resposta
Distribuição de velocidades no espaço entre as placas:
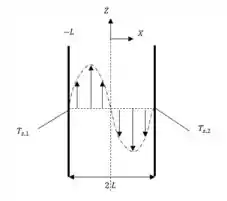
Formas apropriadas para as equações da continuidade, do momento e da energia para o escoamento laminar entre as placas:
A distribuição de temperaturas:
O gradiente de pressão na direção vertical, admitindo que a massa específica seja uma constante correspondente a :
A distribuição de velocidades: