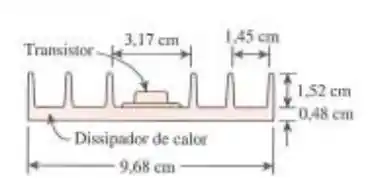
Dissipadores de calor de alumínio com perfil retangular são comumente usados ​​para resfriar componentes eletrônicos. Considere um dissipador de calor de 7,62 cm de comprimento e 9,68 cm de largura cuja seção transversal e dimensões são mostradas na Fig. P9–58. O dissipador de calor é orientado verticalmente e é usado para resfriar um transistor de potência que pode dissipar até 125 W de potência. A superfície traseira do dissipador de calor é isolada. As superfícies do dissipador de calor, se não tratadas, apresentam baixo nível de emissividade (abaixo de 0,1). Portanto, a transferência de calor por radiação a partir do dissipador de calor pode ser negligenciada. Durante um experimento realizado na sala com ar a 22°C, a temperatura da base do dissipador de calor foi medida em 120°C quando a potência de dissipação do transistor foi de 18 W. Considerando que todo o dissipador de calor esteja na temperatura da base, determine o coeficiente médio de transferencia de calor por convecção natural para esse caso.

Bom galera, a área da base é a área disponível para troca de calor que não está ocupada pelas aletas, certo?

Então nós teremos quatro intervalos de 1,45 cm de comprimento com a largura da placa, 7,62 cm, e um intervalo de comprimento igual a 3,17 cm:

De acordo com a geometria da aleta podemos calcular sua área como sendo:

As aletas terão o comprimento da placa:

O comprimento já foi dado na figura:

E quanto a espessura?

Sabemos o comprimento total da placa e sabemos os intervalos entre as aletas, certo? O espaço restante será devido a espessura das seis aletas presentes

Então:

Ou melhor:

Agora é só calcular a área de uma aleta:

Se essa é a área para uma aleta, a área de seis será:

Precisamos achar a transferência de calor, certo?

Mas antes vamos achar a área superficial total:

Agoora sim !!

Beem legal, né!?