Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 28

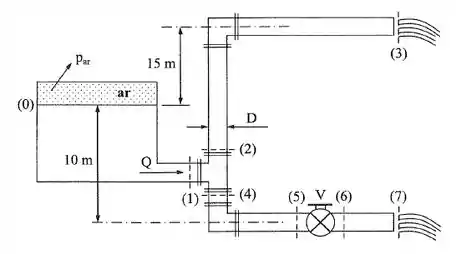
A figura está num plano vertical. Calcular a perda de carga que deve ser introduzida pela válvula V da figura para que a vazão se distribua igualmente nos dois ramais, cujos diâmetros são iguais. Dados: D = 5   c m ; γ H 2 O = 10 4   N / m 3 ; p a r = 0,2   M P a ; Q = 10   L / s ; H p 0,1 = 2   m ; H p 1,2 , 4 = 0 ; H p 2,3 = 3   m ; H p 4,5 = 3   m ; H p 6,7 = 2   m .

Passo 1

Vamos começar o exercício calculando a vazão nos pontos 3 e 7, que segundo o enunciado, devem ser iguais, ou seja, metade da vazão que chega através de 0, então, temos:

Q 3 = Q 0 2 = 10.10 - 3 2 → Q 3 = 0,005   m 3 / s → Q 7 = 0,005   m 3 / s

Agora vamos encontrar a velocidade nos pontos 3 e 7 através da vazão:

Q 3 = v 3 A → v 3 = Q 3 A = Q 3 π D 3 2 4 = 4 ( 0,005 ) π 0,05 2 → v 3 = 2,55   m / s

Como temos a mesma vazão e a mesma seção, então:

v 7 = 2,55   m / s

Passo 2

Agora vamos calcular a carga no ponto 0:

H 0 = v 0 2 2 g + p 0 γ + z 0 = 0 + 0,2.10 6 10 4 + 10 → H 0 = 30   m

Agora, da mesma forma, calculando a carga no ponto 3:

H 3 = v 3 2 2 g + p 3 γ + z 3 = 2,55 2 2 10 + 0 + 25 → H 3 = 25,3   m

E, mais uma vez, vamos calcular a carga no ponto 7:

H 7 = v 7 2 2 g + p 7 γ + z 7 = 2,55 2 2 10 + 0 + 0 → H 7 = 0,3   m

Passo 3

Agora, vamos usar o princípio da conservação da energia para o sistema, dessa forma, temos:

γ Q 0 H 0 = γ Q 0 H p 0,1 + γ Q 3 H p 2,3 + γ Q 7 H p 4,7 + γ Q 3 H 3 + γ Q 7 H 7

Substituindo os valores conhecidos na equação, temos:

10 4 0,01 30 = 10 4 0,01 2 + 10 4 0,005 3 + 10 4 0,005 H p 4,7 + 10 4 0,005 25,3 + 10 4 0,005 0,3

H p 4,7 = 27,4   m

Agora, como encontramos a perda de carga entre os pontos 4 e 7, e o enunciado nos deu a perda de carga entre os pontos 4 e 5 e 6 e 7, podemos escrever a perda de carga da válvula (pontos 5 e 6) como:

H p 5,6 = H p 4,7 - H p 4,5 - H p 6,7 = 27,4 - 3 - 2 → H p 5,6 = 22,4   m

Resposta

H p 5,6 = 22,4   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bocal da figura descarrega 40L / s de um fluido de v = 10 - 4m 2 / s e γ = 8000N / m 3 no canal de seção retangular. Determinar: a velocidade média do fluido no canal;o mínimo diâmetro da seção 1 pa
Num conduto de seção circular escoa água ( ρ = 1000k g / m 3 ). Admite-se que nas seções A e B os diagramas de velocidades sejam os indicados na figura. Supondo P A = P B , determinar:A velocidade méd
Na instalação da figura, a bomba envia 5L / s de água ( γ = 10 4N / m 3 ) para o reservatório superior e uma parte da vazão retorna para o tanque inferior. Dados: P 6 = 100k P a ; H p 6,0 = 25m ; H p
Na instalação da figura, a turbina recebe água do reservatório 0 e a descarrega no reservatório 3 . A turbina aciona diretamente o eixo de uma bomba que eleva a água a 10m de altura, onde é descarrega
No circuito da figura, a potência fornecida ao fluido pela bomba é 7,5k W . O fluido é água ( γ = 10 4N / m 3 ) e o fluido manométrico é mercúrio γ H g = 1,36 × 10 5 . A instalação está num plano hori