Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 59

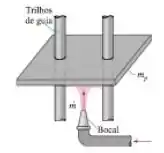
Trilhos de guia vertical quase sem atrito mantêm uma placa de massa m p em posição horizontal, de forma que ela possa deslizar livremente na direção vertical. Um bocal direciona uma corrente de água de área A contra a parte inferior da placa. O jato d’água se espalha no plano da placa, aplicando uma força para cima contra a placa. A vazão da água m ˙   ( k g s ) pode ser controlada. Considere que as distâncias sejam curtas, para que a velocidade seja constante com a altura do jato. (a) Determine a vazão em massa mínima m ˙   necessária para apenas levitar a placa e obter uma relação para a velocidade de estado estacionário da placa que se move para cima para m ˙ > m ˙ m í n (b) no instante t = 0 , a placa está em repouso e o jato d’água com m ˙ > m ˙ m í n   é repentinamente ligado. Aplique o balanço de força na placa e obtenha a integral que relaciona a velocidade ao tempo (não resolva).

Passo 1

Fala aí galera, bora garantir aquele dezão em Mecflu. Primeiramente, tomamos a placa como o sistema. A equação do momento para o fluxo unidimensional constante é:

∑ F = ∑ e x t e r n o β m ˙ V - ∑ i n t e r n o β m ˙ V

Observando que m   =   ρ A V j , onde A é a área da seção transversal do jato de água e W   =   m p g , o fluxo mássico mínimo de água necessário para elevar a placa é determinado definindo a força líquida que atua na placa igual a zero. Logo:

- W = 0 - m ˙ m i n V j

W = m ˙ m i n V j

m p g = m ˙ m i n m ˙ m i n A V j

m ˙ = ρ A m p g

Para m ˙ > m ˙ m i n   é obtida uma relação para a velocidade ascendente em estado estacionário V , configurando o impulso ascendente aplicado pelo jato de água ao peso da placa (durante o movimento constante, a velocidade da placa V é constante e a velocidade do jato de água em relação a placa é V j - V ), temos que:

W = m ˙ V j - V

m p g = ρ A V j - V 2

V j - V = m p g ρ A

Logo:

V = m ˙ ρ A - m p g ρ A

Passo 2

No tempo t   =   0 , a placa está em repouso ( V   =   0 ) e é sujeita a água jato com m ˙ > m ˙ m i n e, portanto, a força líquida que atua sobre ele é maior que a peso da placa e a diferença entre o impulso do jato e o peso acelera a placa para cima. Portanto, a segunda lei de Newton F   =   m a   =   m d V   /   d t , neste caso, pode ser expresso como:

m ˙ V j - V - W = m p a

ρ A V j - V 2 - m p g = m p d V d t

Separando as variáveis ​​e integrando de t   =   0 quando V   =   0 a t   =   t quando V   =   V fornece a integral desejada:

∫ 0 V m p d V ρ A V j - V 2 - m p g = ∫ 0 t d t = t

Resposta

  1. m ˙ = ρ A m p g ;   V = m ˙ ρ A - m p g ρ A
  2. ∫ 0 V m p d V ρ A V j - V 2 - m p g = t
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O escoamento de ar debaixo de um disco de hóquei de mesa é muito complexo, especialmente porque os jatos da mesa de ar atingem o lado inferior do disco em vários pontos, assimetricamente. Uma aproxima
Admita que o mesmo jato d’água permanente do Problema P 3.40 (velocidade do jato, 8m / s , e diâmetro de 10c m ) atinja uma cavidade em forma de concha, semiesférica, como mostra a Figura P A 3.3 . A
Estenda o problema P3.46 para o problema de calcular o centro de pressão L da força normal F n , como mostra na figura abaixo. (No centro de pressão, não são necessários momentos para manter a placa e
O braço de um lava-louças rotativo descarrega a 60°C para seis bocais, como mostrado abaixo. A vazão total é de 11,4 L/min. Cada bocal tem um diâmetro de 4,8 mm. Considerando que as vazões dos bocais
A roda d’água da abaixo está sendo acionada a 200 rpm por um jato de água a 45,7 m/s e 20°C. O diâmetro do jato é de 63 mm. Desprezando as perdas, qual será a potência em hp desenvolvida pela roda? Pa