Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 55

Uma patinadora de 60   k g está de pé sobre o gelo com patins (atrito desprezível). Ela segura uma mangueira flexível (essencialmente sem peso) que direciona uma corrente de água com 2   c m de diâmetro e paralela a seus patins. A velocidade da água na saída da mangueira é de 10   m / s . Se inicialmente estiver parada, determine ( a ) a velocidade da patinadora e a distância que percorrerá em 5   s e ( b ) quanto tempo levará para ela se mover 5   m e a velocidade naquele momento.

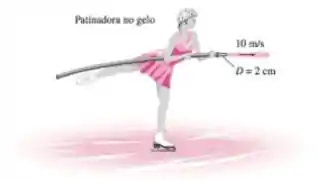
Passo 1

Fala aí galera, bora resolver essa questão de Mecânica dos Fluidos. Primeiramente, temos que o caudal mássico de água através da mangueira é dado por:

m ˙ = ρ V = ρ A V m ˙ = ρ π D 2 4 V m ˙ = 1000 k g m 3 π 0,02   m 2 4 10 m s

m ˙ = 3,14   k g / s  

Passo 2

Com isso, o impulso exercido na patinadora pela corrente da água é simplesmente o fluxo de momento da água, e age na direção inversa, temos:

F = I = m ˙ V = 3,14 k g s 10 m s 1   N 1   k g ∙ m s 2 E = 31,4   N

Então, a aceleração da patinadora é determinada pela 2 ª lei de Newton. Temos:

a = F m a = 31,4   N 60   k g 1   k g ∙ m s 2 1   N a = 0,523   m / s 2

Logo, podemos observar que o Impulso e a acelaração da patinadora são constantes. Assim, podemos encontrar a sua velocidade e a distância percorrida em 5   s . Temos que:

V p = a t V p = 2,62   m / s

E para a distância, temos:

x = 1 2 a t 2 x = 6,54   m

Passo 3

Por fim, o tempo que levará para ela se mover 5   m e a velocidade naquele momento. Fica assim:

x = 1 2 a t 2 5   m = 1 2 0,523 m s 2 t 2 t = 4,4   s

E a sua velocidade vai ser dada por:

V p 2 = a t = 0,523 m s 2 4,4   s V p 2 = 2,3   m / s

Resposta

V p = 2,62   m / s

x = 6,54   m

t = 4,4   s

V p 2 = 2,3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jato de água de 3 cm de diâmetro atinge uma placa normal, como na Figura FE3.5. Se a força necessária para escorar a placa é de 23 N, qual é a velocidade do jato? (a) 2,85 m/s, (b) 5,7 m/s, (c) 8,1
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se a velocidade é V 2 = 8m / s e o atrito é desprezado, qual é a força axial no flange, necessária para manter o bocal fixado ao
Um jato de álcool atinge a placa vertical da Figura P 3.149 . Uma força F ≈ 425N é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule (a) o fluxo de massa de
Um aerofólio com um ângulo de ataque a, como na Figura P 3.150 , proporciona sustentação pelo efeito Bernoulli, porque a superfície inferior retarda o escoamento (alta pressão) e a superfície superior
Água flui por um bocal circular, sai para o ar na forma de um jato e colide com uma placa, como mostra a Figura P 3.151 . A força necessária para manter a placa estacionária é 70N . Admitindo escoamen