Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 86
Um trocador de calor de paredes duplas é usado para transferir calor entre líquidos que escoam através de tubos de cobre semicirculares. Cada tubo tem uma parede com espessura e raio interno , sendo mantido um bom contato entre as duas superfícies planas pela presença de cintas firmemente apertadas. As superfícies externas dos tubos encontram-se isoladas termicamente.
- Se água quente e água fria a temperaturas médias de e escoam pelos tubos adjacentes com , qual é a taxa de transferência de calor por unidade de comprimento do tubo? A resistência térmica de contato entre as paredes é de . Aproxime as propriedades tanto da água quente quanto da água fria por , e Pr = 5,35. Sugestão: A transferência de calor é intensificada pela condução através das porções semicirculares das paredes dos tubos e cada porção pode ser subdividida em duas aletas planas com extremidades adiabáticas.
- Usando o modelo térmico desenvolvido para a parte (a), determine a taxa de transferência de calor por unidade de comprimento quando os fluidos forem o etilenoglicol. Também, qual será o efeito sobre a taxa de transferência de calor ao se fabricar o trocador com uma liga de alumínio? O aumento da espessura das paredes dos tubos trará um efeito favorável?
Passo 1
Essa é daquelas de acabar com o pequi de Goiás ein galera !!
Mas com calma nós venceremos !!
A transferência de calor entre dois fluidos pode ser escrita em função da resitencia à transferência de calor, certo?
Vamos ver como:
Vamos fazer uma análise do que está acontecendo aqui para poder descobrir a resistência total:
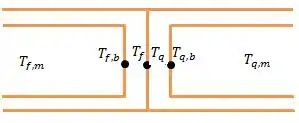
Então a situação será a seguinte:
Onde a resistência equivalente nós vamos expressar como a resistência a receber o calor da aleta e a convectiva do fluido:
Para achar as resistências convectivas nós precisamos dos coeficientes convectivos, mas como?
O primeiro passo é o Reynolds e descobrir como é o escoamento:
Nós não temos o diâmetro hidráulico, mas ele pode ser escrito como:
Colocando em Reynolds:
Lembrando que o perímetro nestes casos é dado por:
Então:
Quando assumimos que a temperatura de saída será próxima de 300 K olhamos na Tabela A.4 para a água:
E na Tabela A.1 para o cobre:
Agora nós conseguimos achar Reynolds:
Como Reynolds é maior que 2300 o fluxo é turbulento!!
Passo 2
Como descobrimos que o fluxo é turbulento podemos usar a correlação de Dittus – Boelter para o resfriamento:
Lembrando que:
E substituindo:
Substituindo a área e o perímetro:
Lançando nossos dados:
Com isso nós conseguimos calcular as resistências convectivas, dadas por:
Como queremos analisar o calor por 1 m de comprimento:
Passo 3
A próxima resistência que vamos achar é a da aleta:
Se:
Substituindo:
Para estas condições nós podemos aproximar o perímetro da superfície da aleta por:
E a sua área:
Onde t é a espessura, ok?
O comprimento da aleta pode ser aproximado pela equação:
Agora vamos colocar nossos dados na fórmula:
Passo 4
Agora nós vamos achar a resistência condutiva:
A última resistência é a de contato:
O problema nos disse que:
Então:
Shooow !! Agora vamos calcular a resistência total, mas antes a equivalente, certo?
Agora sim a total:
E com isso achar a troca de calor ficou molezinha !!
Ufaaaa !! Mas ainda não acabamos, não é?
Passo 5
A letra (b) pede para fazermos a mesma coisa e analisarmos três situações diferentes: usando etilenoglicol, quando o trocador é de liga de alumínio e quando a espessura das paredes dos tubos é maior!
Faremos tudo isso de novo, mas agora que vocês já sabem como fazer eu vou lançar todas estas fórmulas no software IHT e achar o calor para cada um destes casos:
Tabelinha bem prática que resume tudo que precisávamos fazer !!
E agora sim, acabamooos !!
Resposta
