Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 109
Considere o arranjo de resfriamento com microcanais do Problema 8.107. Entretanto, ao invés de supor o chip inteiro e a cobertura a uma temperatura uniforme, adote uma abordagem mais conservativa (e realística), que especifica uma temperatura de = 350 K na base dos canais (x = 0) e permite uma diminuição da temperatura com o aumento de x ao longo das paredes laterais de cada canal.
(a) Para as condições operacionais especificadas no Problema 8.107 e uma condutividade térmica do chip de = 140 W/(m·K), determine a temperatura de saída da água e a dissipação de potência no chip. A transferência de calor das laterais do chip para a vizinhança e da parede lateral de um canal para a cobertura podem ser desprezadas. Observe que o espaçamento entre os canais, δ = S – W, é o dobro do espaçamento entre a parede lateral de um canal externo e a superfície externa do chip. O passo dos canais é S = L/N, com L = 10 mm sendo a largura do chip e N = 50 o número dos canais.
(b) A geometria do canal especificada no Problema 8.107 e usada na parte (a) não é otimizada e taxas de transferências de calor maiores podem ser dissipadas através do ajuste de dimensões relacionadas entre si. Considere o efeito da redução do passo até valores de S = 100 μm, mantendo uma largura de W = 50 μm e uma vazão por canal de .
Passo 1
Beleza! Vamos começar esse exercício assumindo a temperatura média da água no interior do canal de 300 K, dessa forma, teremos , com isso vamos recorrer à tabela A.6 do apêndice A para pegar as propriedades da água nessa temperatura, então teremos:
Agora, nesse exercício teremos as laterais dos microcanais agindo como se fossem aletas. Vamos calcular o passo S dos canais através da equação fornecida no enunciado, onde teremos:
Com isso, o espaçamento entre os canais será:
Agora, como vamos tratar as laterais dos microcanais como aletas, temos que a resistência térmica da célula pode ser encontrada através da equação 3.108, dada para um conjunto de aletas, onde temos:
Onde nós temos que:
Substituindo os valores conhecidos, chegamos em:
Passo 2
Agora vamos calcular o diâmetro hidráulico para o nosso sistema, que será dado por:
Então, com isso, podemos encontrar o número de Reynolds, que será dado por:
Sabemos que a vazão mássica pode ser escrita como:
Substituindo essa expressão na equação para Reynolds e substituindo os valores conhecidos, temos:
Dessa forma, sabemos que o escoamento será laminar.
Passo 3
Com o número de Reynolds encontrado no passo 2, temos que o escoamento é laminar. Com isso, vamos consultar a tabela 8.1 vista nessa seção e apresentada a seguir para obter no número de Nusselt para o escoamento:
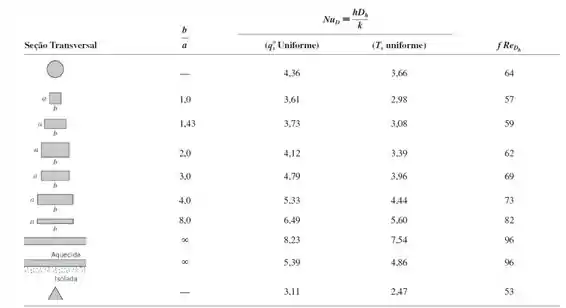
Então, precisamos calcular a razão b/a, onde teremos:
E, como temos uniforme, então no nosso caso teremos:
Com isso, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte relação:
Substituindo os valores conhecidos, temos:
Agora, com isso podemos calcular a eficiência de uma aleta, dada por:
Onde temos:
Substituindo os valores conhecidos, temos:
Então, a eficiência para uma aleta será:
Passo 4
Agora, com a eficiência da aleta, podemos calcular a eficiência geral de superfície, dada por:
Com esse valor, podemos calcular a resistência térmica descrita lá no passo 1, onde teremos:
E, agora, podemos utilizar a equação 8.45b vista nesse capítulo para encontrar a temperatura média de saída. Dessa forma, teremos:
Como no nosso caso, conhecemos a temperatura da superfície externa e ela é constante, a equação se torna:
Substituindo os valores conhecidos, chegamos em:
Agora, com a temperatura de saída, conseguimos encontrar a potência dissipada pelo chip, através do calor trocado com a água, dada por:
Substituindo os valores conhecidos, temos:
Passo 5
Agora, para a letra (b), onde temos uma redução nas dimensões de passo e mantendo a largura , e com isso, teremos N = 100 microcanais. Nesse caso então, o espaçamento entre os canais será:
Agora devemos repetir os cálculos feitos para a letra (a), então, vamos lá, começando pela área total, como não houve alteração em H e W, a área será a mesma, ou seja:
O diâmetro hidráulico também será o mesmo, e por consequência o número de Reynolds, então teremos:
Teremos também o mesmo valor de Nusselt e coeficiente convectivo, onde teremos:
O que será diferente será a eficiência de cada aleta, dada por:
Onde m é dada por:
Substituindo os valores conhecidos, temos:
Então a eficiência de cada aleta será:
Passo 6
Agora, com a eficiência da aleta, podemos calcular a eficiência geral de superfície, dada por:
Com esse valor, podemos calcular a resistência térmica descrita lá no passo 1, onde teremos:
Agora, calculando a temperatura média de saída teremos:
Agora, com a temperatura de saída, conseguimos encontrar a potência dissipada pelo chip, através do calor trocado com a água, dada por:
Substituindo os valores conhecidos, temos: