Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 8.Problemas - Ex. 65

Um trocador de calor de paredes duplas é usado para transferir calor entre líquidos que escoam através de tubos de cobre semicirculares. Cada tubo tem uma parede com espessura t = 3   m m e raio interno r i = 20   m m , sendo mantido um bom contato entre as duas superfícies planas pela presença de cintas firmemente apertadas. As superfícies externas dos tubos encontram-se isoladas termicamente.

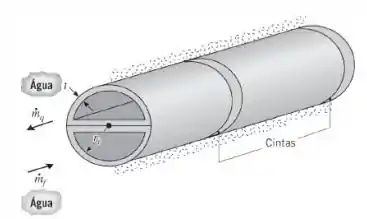
(a) Se água quente e água fria a temperaturas médias de T q , m = 330   K e T f , m   =   290   K escoam pelos tubos adjacentes com m ˙ q = m ˙ f = 0,2   k g / s , qual é a taxa de transferência de calor por unidade de comprimento do tubo? A resistência térmica de contato entre as paredes é de 10 - 5   m 2   K / W . Aproxime as propriedades tanto da água quente quanto da água fria por μ = 800 × 10 – 6   k g / ( s · m ) , k = 0,625   W / ( m · K ) e P r = 5,35 .

S u g e s t ã o : A transferência de calor é intensificada pela condução através das porções semicirculares das paredes dos tubos e cada porção pode ser subdividida em duas aletas planas com extremidades adiabáticas.

(b) Usando o modelo térmico desenvolvido para a parte (a), determine a taxa de transferência de calor por unidade de comprimento quando os fluidos forem o etilenoglicol. Também, qual será o efeito sobre a taxa de transferência de calor ao se fabricar o trocador com uma liga de alumínio? O aumento da espessura das paredes dos tubos trará um efeito favorável?

Passo 1

Opa, vamos resolver mais uma questão juntos!

Então, fica ligado!

Começamos o nosso problema obtendo a seguinte propriedade para o cobre sob a temperatura adotada de 300   K na Tabela A.1:

k = 400   W / m ⋅ K

Algumas propriedades da água que utilizaremos já foram dadas pelo enunciado:

μ = 800 × 10 – 6   k g / ( s · m )

k = 0,625   W / ( m · K )

P r = 5,35

Bora para os cálculos!

Passo 2

Letra a)

Temos que a taxa de transferência de calor entre dois fluídos em função da resistência é dada por:

q ' = T m , q - T m , f R t o t '

Com a resistência total sendo:

R t o t ' = 2 R e q + R c o n d + R t , c

E a resistência equivalente:

R e q = 1 R a l e t + 1 R c o n v - 1

Agora devemos calcular essas resistências!

Passo 3

Calculando o número de Reynolds:

R e D = ρ u m D h μ = m ˙ D h μ A c

Com o diâmetro hidráulico:

D h = 4 A c P

E:

P = 2 r i + π r i

A c = π r i 2

Temos:

R e D = m ˙ D h μ A c = 4 m ˙ μ 2 r i + π r i

Substituindo os dados:

R e D = 4 ⋅ 0,2 800 × 10 - 6 ⋅ 2 ⋅ 0,02 + π ⋅ 0,02

R e D = 9725

F l u x o   T u r b u l e n t o

Passo 4

Calculando o coeficiente convectivo utilizando a equação do número de Nusselt obtida pela correlação de Gnielinski para R e D < 10000 :

N u D = h D h k = f 8 ⋅ R e D - 1000 ⋅ P r 1 + 12,7 ⋅ f 8 1 2 ⋅ P r 2 3 - 1 = 69,9

Com:

f = 0,79 ⋅ ln ⁡ R e D - 1,64 - 2

f = 0,79 ⋅ ln ⁡ 9725 - 1,64 - 2

f = 0,0317

Assim:

h = N u D ⋅ k D h = N u D ⋅ k ⋅ π + 2 2 π r i

h = 69,9 ⋅ 0,625 ⋅ π + 2 2 ⋅ π ⋅ 0,02

h = 1790

Passo 5

Calculando as resistências:

- Convectiva:

R c o n v = 1 2 r i h = 1 2 ⋅ 0,04 ⋅ 1790 = 0,014   m ⋅ K / W

- Aleta:

R a l e t = θ b q a l e t ' = 1 h P ' k A c ' 1 2 tanh ⁡ h P k A c 1 2 L  

Calculando os dados:

L = π r i 2 = 0,0314   m

A c = 2 t ⋅ 1 = 0,006   m 2

P = 2,1   m

Assim:

h P ' k A c ' = 1790 ⋅ 2 ⋅ 400 ⋅ 0,006 1 2 = 92,7   W / k ⋅ W

h P k A c 1 2 L = 1790 ⋅ 2 400 ⋅ 0,006 1 2 ⋅ 0,03142 = 1,21   m

Desse modo:

R a l e t = 1 92,7 ⋅ tanh ⁡ 1,21

R a l e t = 0,0129   m ⋅ K / W

- Condutiva:

R c o n d ' = t 2 k r i = 0,003 2 ⋅ 400 ⋅ 0,02

R c o n d ' = 1,875 × 10 - 4 m ⋅ K / W

-Contato:

R t , c ' = R t . c ' ' 2 r i = 10 - 5 2 ⋅ 0,02 = 2,5 × 10 - 4   m ⋅ K / W

Passo 6

Calculando a resistência equivalente:

R e q ' = 1 R a l e t + 1 R c o n v - 1

R e q ' = 1 0,0129 + 1 0,014 - 1

R e q ' = 6,7 × 10 - 3   m ⋅ K / W

Calculando a resistência total:

R t o t ' = 2 R e q + R c o n d + R t , c

R t o t ' = 2 ⋅ 6,7 × 10 - 3 + 1,875 × 10 - 4 + 2,5 × 10 - 4

R t o t ' = 0,0140   m ⋅ K / W

Por fim, calculando a taxa de transferência de calor:

q ' = T m , q - T m , f R t o t '

q ' = 330 - 290 0,0140

q ' = 2850   W / m

Bora para a letra (b)!

Passo 7

Para a segunda parte do nosso problema devemos obter algumas propriedades dos novos materiais e considerar algumas coisas:

C a s o   1 : Á g u a   e   C o b r e   400 W m ⋅ K ,   t = 3   m m

C a s o   2 : E t i l e n o   G l i c o l   e   C o b r e   400 W m ⋅ K ,   t = 3   m m

C a s o   3 : Á g u a   e   A l u m i n i o   117 W m ⋅ K ,   t = 3   m m

C a s o   4 : Á g u a   e   C o b r e   400 W m ⋅ K ,   t = 4   m m

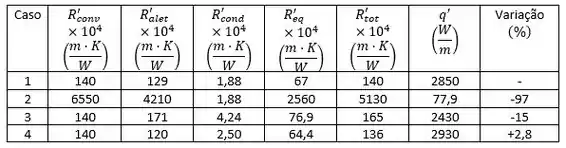
Repetindo os passos da Letra (a), obtemos os seguintes resultados expostos na tabela abaixo:

Até a próxima questão!

Resposta

a )   q ' = 2850   W / m

b )   T a b e l a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6 - Estime o coeficiente de transferência de calor na ebulição nucleada em piscina de água fervendo a pressão atmosférica sobre a superfície externa de um tubo revestido com uma camada de platina, que
Água a pressão atmosférica está em ebulição sobre a superfície de um grande tubo horizontal de cobre. O fluxo térmico é 90% do valor crítico. A superfície do tubo encontra-se inicialmente riscada; ent
O fundo de uma panela de cobre, que tem 150 mm de diâmetro, é mantido a 115°C por um elemento de aquecimento elétrico. Estime a potência necessária para ferver a água nesta panela. Determine a taxa de
Uma forma de resfriar chips nas placas de circuito de um computador é colocar as placas em quadros de metal que permitem a passagem eficiente da condução térmica para placas frias, que suportam o arra
Refrigerante-134a é transportado a 0,1 kg/s através de um tubo de Teflon com diâmetro interno Di = 25 mm e diâmetro externo De = 28 mm, enquanto ar atmosférico a V = 25 m/s e 300 K escoa em escoamento