Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 58
Uma das demonstrações populares em feiras de ciências envolve a suspensão de uma bola de ping-pong por um jato de ar dirigido para cima. As crianças ficam encantadas observando que a bola sempre retorna para o centro do jato de ar quando ela é empurrada para o lado com o dedo. Explique esse fenômeno usando a equação de Bernoulli. Determine também a velocidade do ar se a bola tiver uma massa de 2,6 g e um diâmetro de 3,8 cm. Suponha que o ar está a 1 atm e 25 °C.
Passo 1
Antes de começar esse exercício, nós vamos lá na tabela A.9 do apêndice A para pegar as propriedades de interesse do ar nas condições de 1 atm e 25 °C, de onde teremos:
Beleza! Nós sabemos então que a velocidade terminal de um objeto em queda livre, ou nesse caso, a suspensão de um objeto ou partícula no ar, ocorre quando a força de arrasto se iguala ao peso do objeto em queda menos a força de empuxo exercida pelo meio em que está, ou seja, resumindo isso, temos:
Sabendo que a força de arrasto é dada por:
Em que, nesse caso, a área corresponde a área transversal da base do cilindro, ou seja:
Substituindo essa expressão na equação da força de arrasto, chegamos em:
Agora, sabendo que o peso da bola pode ser escrito como:
E, que, por sua vez, a força de empuxo é dada pela força exercida pelo ar na bola, ou seja:
Passo 2
Agora então, nós vamos substituir as expressões encontradas para a força de arrasto, para o peso da partícula de pó e para a força de empuxo lá na equação do passo 1, então teremos:
Substituindo os valores conhecidos e isolando a velocidade dessa equação, chegamos em:
Passo 3
Agora, como precisamos determinar o coeficiente de arrasto, o que, por sua vez, depende do número de Reynolds. Então, sabendo que Reynolds é dado por:
Substituindo os valores conhecidos nessa equação, teremos:
Precisamos da velocidade para encontrar o número de Reynolds para poder encontrar o coeficiente de arrasto e, por sua vez, determinar a velocidade real. Então, estamos em um problema clássico de iteração. Nesse caso, precisamos chutar um valor de , vamos começar com:
Para esse valor de velocidade, nosso Reynolds será:
Então, agora precisamos ir lá na figura 11-34 que vimos nesse capítulo para encontrar o coeficiente de arrasto em função do número de Reynolds que encontramos. Então com o auxílio da figura 11-34 a seguir:
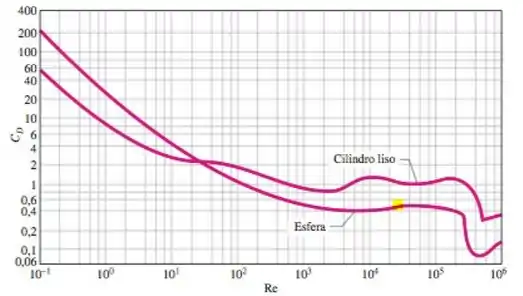
Para o nosso número de Reynolds então, conforme destacado no gráfico acima, teremos:
Com isso, substituindo esse valor na equação para a velocidade encontrada no passo 2, temos:
Passo 4
Agora vamos realizar mais uma iteração, então, com o valor de velocidade encontrado no passo 3, teremos o seguinte número de Reynolds:
Então, agora precisamos ir lá na figura 11-34 que vimos nesse capítulo para encontrar o coeficiente de arrasto em função do número de Reynolds que encontramos. Então com o auxílio da figura 11-34 a seguir:
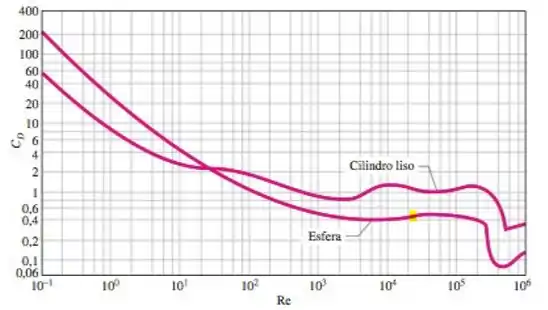
Para o nosso número de Reynolds então, conforme destacado no gráfico acima, teremos:
Com isso, substituindo esse valor na equação para a velocidade encontrada no passo 2, temos:
Como houve pequena variação do valor da velocidade comparado ao valor encontrado no passo 3, podemos tomar essa velocidade como sendo a velocidade do escoamento de ar.