Um tubo circular de água tem uma expansão abrupta do diâmetro para . A pressão e a velocidade média da água no tubo menor são e , respectivamente, e o escoamento é turbulento. Aplicando as equações da continuidade, do momento e da energia e desprezando os efeitos dos fatores de correção para a energia cinética e para o fluxo de momento mostre que o coeficiente de perda para a expansão repentina é e calcule e para este caso.

O nosso diagrama ficará assim:

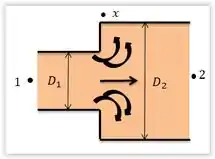
Aplicamos a equação de continuidade:

Como a densidade é constante, então:

Certo, até ai tudo bem, temos a primeira equação. Agora, pela conservação de momento em um regime permanente, temos:

Organizamos as forças atuando no sistema e, como desprezamos os efeitos dos fatores de correção para a energia cinética e para o fluxo de momento, temos e .

Temos que ter atenção para a expansão que nós chamamos de , é como se tivéssemos o ponto , e um “meio” ponto de . Portanto:

Nesse caso, a seção também ocupa o ponto , logo

Como estamos usando a equação de continuidade, para a vazão mássica tanto faz o ponto ou o ponto , escolhemos o :

Assim, do passo , aplicamos na equação acima:

Para a equação de energia, como não há bomba nem turbina, temos e . Assim:

Como e considerando as expressões finais dos passos, vamos substituindo:

Isolando :

Com a expressão anterior, vamos calcular o :

Assim, e .

E por fim, calculamos :

Prontinho!!