Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 31
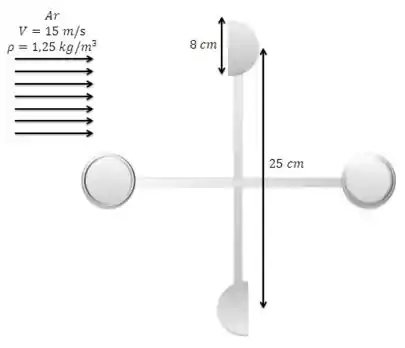
Uma turbina eólica com duas ou quatro conchas hemisféricas conectadas a um pivô é usada comumente para medir a velocidade do vento. Considere uma turbina de vento com duas conchas de de diâmetro com uma distância de centro a centro de , conforme mostra a Figura . O pivô está preso devido a um defeito mecânico e as conchas não estão girando. Para um vento com velocidade de e densidade do ar de , determine o torque máximo que a turbina aplica ao pivô.
Passo 1
Temos ar escoando sobre duas conchas. Para uma corrente de velocidade e densidade devemos obter o torque que será gerado.Tudo bem?
Para calcular o torque usaremos a relação:
Em que é a distância do centro da concha ao centro da turbina. Precisamos então determinar a força de arraste que é exercida sobre as conchas. Vamos lá?
Passo 2
Para chegar à força de arraste nosso próximo passo será obter o coeficiente de arraste.
Pela Tabela o coeficiente de arraste para a concha aberta na direção da corrente é enquanto que o coeficiente de arraste para a concha aberta na direção oposta ao escoamento é .
Para calcular a força de arraste podemos aplicar a relação:
Passo 3
Para finalizar, vamos calcular o torque. A distância entre o centro da concha e o centro da turbina é . Então:
Resposta
O torque sobre a turbina é .