Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 14

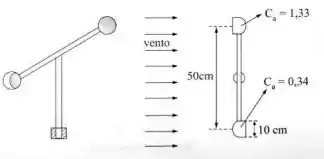
Um anemômetro, utilizado para medir a velocidade do vento, consiste de duas semiesferas ocas montadas em sentidos opostos sobre dois braços iguais, que podem girar livremente quando montados sobre um eixo vertical. Qual é o momento necessário para manter o dispositivo estacionário, quando o vento tem uma velocidade de 36 km/h? ( ρ a r = 1   k g / m 3 )

Passo 1

Os dados da questão:

  • Diâmetro: d = 10   c m = 0,1   m
  • Haste: L = 50   c m = 0,5   m
  • Coeficientes de arrasto: C a 1 = 0,34 e C a 2 = 1,33
  • Velocidade do vento: v 0 = 36   k m / h = 10   m / s

Passo 2

A área de referência das esferas são:

A = π d 2 4 = π ⋅ 0,1 2 4 = 2,5 π ⋅ 10 - 2   m 2

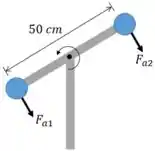
Vamos calcular as forças de arrasto:

Força de arrasto 1:

F a 1 = C a 1 ⋅ ρ ⋅ v 0 2 2 A = 0,34 ⋅ 1 ⋅ 10 2 2 2,5 π ⋅ 10 - 2

F a 1 = 4,2 5 π ⋅ 10 - 2

Força de arrasto 2:

F a 2 = C a 2 ⋅ ρ ⋅ v 0 2 2 A = 1,33 ⋅ 1 ⋅ 10 2 2 2,5 π ⋅ 10 - 2

F a 2 = 16,625 π ⋅ 10 - 2

Passo 3

Vamos finalizar a questão calculando o somatório de momento no pino:

∑ M = 0 ⇒ M + F a 1 ⋅ L 2 - F a 2 ⋅ L 2 = 0

M = F a 2 ⋅ L 2 - F a 1 ⋅ L 2

M = 16,625 π ⋅ 10 - 2 ⋅ 0,5 2 - 4,2 5 π ⋅ 10 - 2 ⋅ 0,5 2

M = 9,72 ⋅ 10 - 2   N ⋅ m

Resposta

M = 9,72 ⋅ 10 - 2   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um antigo avião carrega 50 m de fios de corda estirados na direção normal à direção do movimento. O diâmetro do fio é 5 mm. Estime a economia máxima de potência decorrente de uma carenagem ótima dos f
Um avião, com massa de 4500 kg, voa a 240k m / h em uma trajetória circular de elevação constante. O círculo de voo tem raio de 990m . O avião tem área de sustentação de 23m 2 e está equipado com aero
As bolas de golfe americana e inglesa têm diâmetros ligeiramente diferentes mas a mesma massa (veja os Problemas 1.39 e 1.42). Suponha que um golfista profissional golpeia, com um taco em tê, cada tip
Um projeto de graduação envolve a construção de um modelo de um avião ultraleve. Alguns estudantes propõem fazer um aerofólio, a partir de uma folha rígida de plástico, de 1,5 m de comprimento e 2 m d
O ângulo de voo planado, sem motor, é tal que a sustentação, o arrasto e o peso estão em equilíbrio. Mostre que o ângulo de inclinação de voo planado, θ , é tal que θ= C D C L . O ângulo mínimo de voo